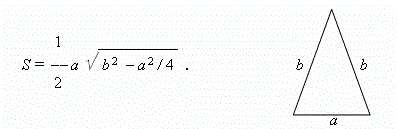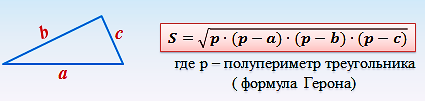Результаты исследования обучающихся в проекте: мир площадей
Материал из Wiki Mininuniver
Версия от 11:50, 17 июня 2019; Egor Savin (обсуждение | вклад) (→Площадь четырехугольника, около которого описывается круг:)
Содержание
- 1 Авторы и участники проекта
- 2 Тема исследования группы
- 3 Проблемный вопрос (вопрос для исследования)
- 4 Гипотеза исследования
- 5 Цели исследования
- 6 Результаты проведённого исследования
- 6.1 Формулы для вычисления площадей плоских фигур:
- 6.1.1 Площадь квадрата:
- 6.1.2 Площадь прямоугольника:
- 6.1.3 Площадь ромба:
- 6.1.4 Площадь параллелограмма:
- 6.1.5 Площадь трепеции:
- 6.1.6 Площадь произвольного четырехугольника
- 6.1.7 Площадь четырехугольника, около которого описывается круг:
- 6.1.8 Площадь равнобедренного треугольника:
- 6.1.9 Площадь равностороннего треугольника:
- 6.1.10 Площадь прямоугольного треугольника:
- 6.1.11 Площадь произвольного треугольника:
- 6.1 Формулы для вычисления площадей плоских фигур:
- 7 Вывод
- 8 Полезные ресурсы
- 9 Другие документы
Авторы и участники проекта
Участники группы: "Исследователи площадей многоугольников"
Тема исследования группы
Площади многоугольников
Проблемный вопрос (вопрос для исследования)
Как считаются площади различных многоугольников?
Гипотеза исследования
Мы считаем, что у каждого многоугольника есть своя формула нахождения площади и некоторые из них связаны между собой
Цели исследования
1.Расширить знания учащихся о треугольниках, квадратах, прямоугольниках и трапециях, их элементах и их площадях как с математической точки зрения;
2.Развить творческую активность учащихся, умение делать обобщения на основе данных, полученных в результате исследований;
3.Развить познавательную деятельность учащихся, которая в свою очередь, способствует развитию разносторонней личности;
4. Воспитывать у учащихся стремление к самосовершенствованию, удовлетворению познавательных потребностей.
Результаты проведённого исследования
Формулы для вычисления площадей плоских фигур:
Площадь квадрата:

Где a-сторона, d-диагональ.
Площадь прямоугольника:
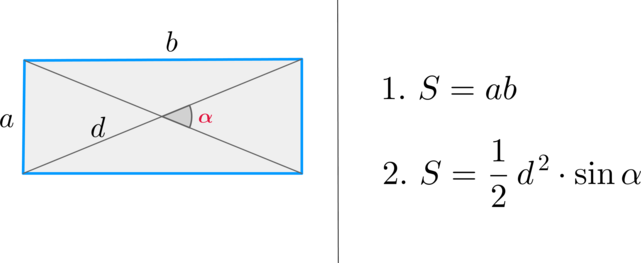
Где a,b-стороны, d-диагональ.
Площадь ромба:
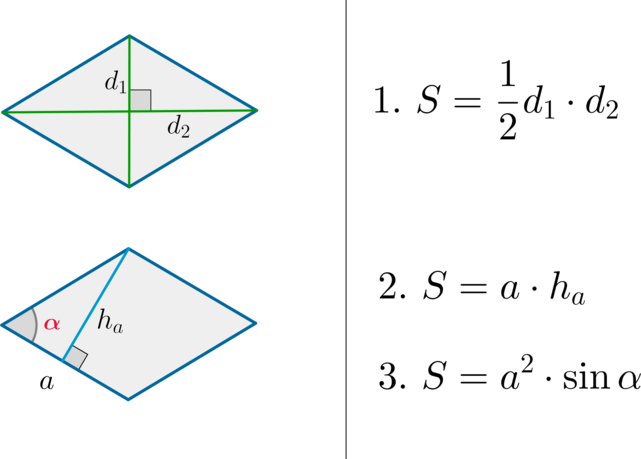
Где d-диагонали, a-сторона.
Площадь параллелограмма:
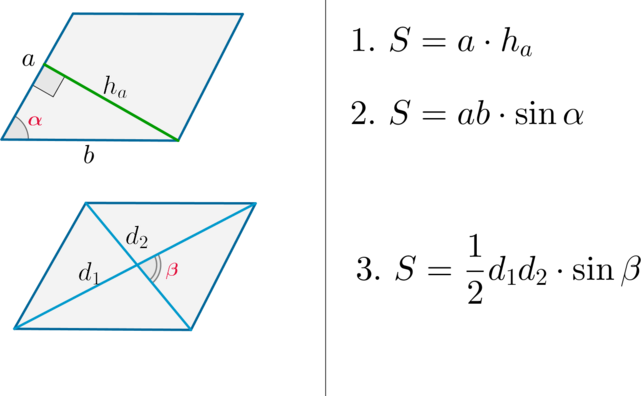
Где a,b-стороны, h-высота.
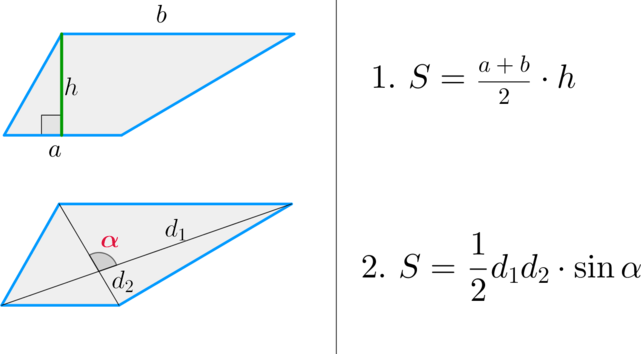
Площадь трепеции:
Где d-диагонали.
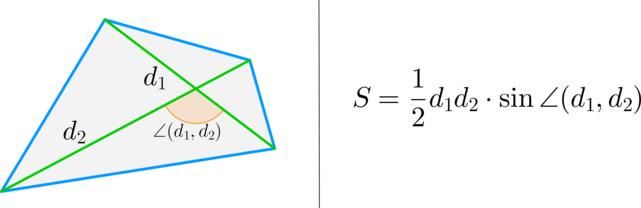
Площадь произвольного четырехугольника
Площадь четырехугольника, около которого описывается круг:
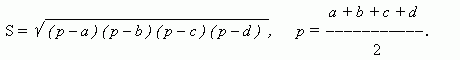
Где a,b,c,d -стороны, p-полупериметр.