Результаты исследований группы Инженеры в проекте Вычисляем рассуждения

Название проекта

Учебный проект Вычисляем рассуждения

Авторы и участники проекта

1. Плеханов Семён Петрович
2. Лабзин Андрей begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting begin_of_the_skype_highlighting     end_of_the_skype_highlighting Федорович
3. Гришин Евгений Анатольевич
4. Кислицкий Илья Станиславович
5. Комаров Иван Александрович

Тема исследования группы

Как аппарат математической логики применяется в современной электронно-вычислительной технике?

Поставленные задачи

1) Создать группу <<Инженеры>> на Google для организации взаимодействия в ходе исследовательской работы.
2) Осуществить совместный подбор ссылок на Интернет-ресурсы и поиск информации в печатных изданиях по теме исследования.
3) Провести анализ полученной информации по теме исследования и ответить на вопросы:
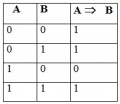
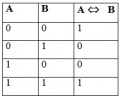
а) как язык классической математической логики находит применение при построении релейно-контактных схем?
б) что такое нечеткая логика и в каких областях она применяется?
4) Сформулировать выводы по результатам исследования.
5) Оформить результаты исследования.

Проблемный вопрос (вопрос для исследования)

Как происходит взаимодействие логической части программы с её физической начинкой.

Гипотеза исследования

Проанализировать возможности языка математической логики в современной электронно-вычислительной технике.
Как используются в технике :

• Полусумматор.
  
• Сумматор.
  
• Триггер.
  

Цели исследования

Провести анализ возможностей использования языка математической логики в современной электронно-вычислительной технике.

Результаты исследования

Нами была создана гугл группа

• 

  КОНЪЮНКЦИЯ (логическое умножение)

• 

  ДИЗЪЮНКЦИЯ (логическое сложение)

• 

  ИМПЛИКАЦИЯ (логическое следование)

• 

  ИНВЕРСИЯ (отрицание)

• 

  ЭКВИВАЛЕНЦИЯ (равнозначность)

Полусумматор — логическая схема имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Полусумматор используется для построения двоичных сумматоров. Полусумматор позволяет вычислять сумму A+B, где A и B — это разряды двоичного числа, при этом результатом будут два бита S,C, где S — это бит суммы по модулю, а C — бит переноса.

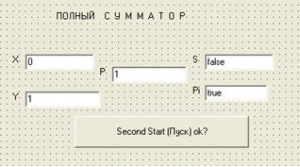
Сумматор — логический операционный узел, выполняющий арифметическое сложение двоичных, троичных или n-ичных кодов двух (бинарный), трёх (тринарный) или n чисел (n-нарный). При арифметическом сложении выполняются и другие дополнительные операции: учёт знаков чисел, выравнивание порядков слагаемых и тому подобное.

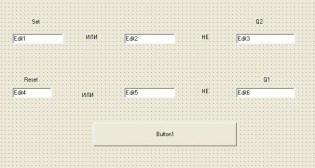
Триггер — класс электронных устройств, обладающих способностью длительно находиться в одном из двух или более устойчивых состояний и чередовать их под воздействием внешних сигналов. Каждое состояние триггера легко распознаётся по значению выходного напряжения. По характеру действия триггеры относятся к импульсным устройствам — их активные элементы (транзисторы, лампы) работают в ключевом режиме, а смена состояний длится очень короткое время.

Полусумматор	Полный сумматор	Триггер
var x,y,Pi,P,S:Boolean; procedure TForm1.Button1Click(Sender: TObject); begin x:=strtobool(edit5.text); y:=strtobool(edit6.text); Pi:=strtobool(edit7.text); P:=(not x and y and Pi)or(x and not y and Pi) or(x and y and not Pi)or(x and y and Pi); S:=(not x and not y and Pi)or(not x and y and not Pi) or(x and not y and not Pi)or(x and y and Pi); edit8.text:=booltostr(S,true); edit9.text:=booltostr(P,true); end; end.	var x,y,s,p,pi :boolean; procedure TForm1.Button1Click(Sender: TObject); begin x:=strtobool(edit5.Text); y:=strtobool(edit6.Text); P:=strtobool(edit7.Text); S:=(not x and not y and p) or (not x and y and not p) or(x and not y and not p) or (x and y and p); Pi:=(not x and y and p) or (x and not y and p) or(x and y and not p) or(x and y and p); edit8.text:=booltostr(s,true); edit9.text:=booltostr(pi,true); end; end.	var S,R,Or1Out,Not1out,or2out,not2out:boolean procedure TForm2.Button1Click(Sender: TObject); begin S:=StrToBool(editset.text); R:=StrToBool(editreset.text); or1out:=s or not2out; not1out:=not or1out; or2out:=not1 out or r; not2out:=bot or2out; editor1out.text:=booltostr(or1out,true); editor2out.text:=booltostr(or2out,true); editq2.text:=booltostr(not1out,true); editq1.text:=booltostr(not2out,true); end; end.

Полезные ресурсы

Математическая логика

Сетунь(компьютер)

Логика в информатике

Алгебра логики и логические основы компьютера

Полусумматор

Сумматор

Триггер