Результаты исследований группы Инженеры в проекте Вычисляем рассуждения: различия между версиями
| Строка 32: | Строка 32: | ||
== Гипотеза исследования == | == Гипотеза исследования == | ||
Мы предполагаем, что математическая логика<br> | Мы предполагаем, что математическая логика<br> | ||
| − | имеет достаточно широкое применение в современной электронно-вычислительной технике(Логические элементы) | + | имеет достаточно широкое применение в современной электронно-вычислительной технике(Логические элементы). |
| − | |||
| − | |||
| − | |||
==Цели исследования== | ==Цели исследования== | ||
| Строка 47: | Строка 44: | ||
Был произведён подбор ссылок на сервисе [http://bobrdobr.ru/people/cl0Ne/ ДоброгоБобра] | Был произведён подбор ссылок на сервисе [http://bobrdobr.ru/people/cl0Ne/ ДоброгоБобра] | ||
| + | |||
| + | [http://ru.wikipedia.org/wiki/Математическая_логика Математическая логика] (или символическая логика) - область знания, которая сложилась в результате применения в логике формальных методов математики и логического исследования математических рассуждений и доказательств. В математической логике логические процессы изучаются посредством их отображения в формализованных языках, или логических исчислениях. Наряду с изучением формального строения логических исчислений (Логический синтаксис) в математической логике встает также задача рассмотрения отношений между исчислениями и теми содержательными областями, которые служат их интерпретациями и моделями. Эта задача обрисовывает проблематику логической семантики. Логический синтаксис и семантика включаются в металогику - теорию средств описания, предпосылок и свойств логических исчислений. Некоторые исходные понятия математической логике содержатся уже в учении мегаро-стоической школы (3 в. до н. э.). Саму же идею логического исчисления, по-видимому, впервые сформулировал Лейбниц. Однако как самостоятельная дисциплина математическая логика оформилась в середине 19 в. благодаря работам Буля. С Буля начинается развитие так называемой алгебры логики. Другое направление разработки математической логики ставшее определяющим, начинается с конца 19 века в связи с потребностями математики в обосновании своих понятий и способов доказательств. У истоков этого направления лежат труды Фреге. Значительный вклад в его развитие внесли Рассел, Уайтхед и Гильберт. В этот период создаются фундаментальные логические системы математической логики - классические исчисление высказываний и исчисление предикатов. Крупные результаты, определившие современное состояние математической логики, были получены в. 30-х гг. Гёделем. Тарским, А. Чёрчем. Современный этап математической логики характеризуется исследованием разнообразных видов логических исчислений, интересом к проблемам семантики и вообще металогики, к вопросам специальных математических и технических приложений логики. В связи с задачами обоснования математики наряду с работами в области классической математической логике разрабатывается интуиционистская и конструктивная логика. С анализом оснований логики связаны исследования по комбинаторной логике. Ведутся исследования в области многозначных, модальных и релевантных логик. Математическая логика оказала влияние на развитие ряда разделов современной математики, общей алгебры, теории алгоритмов, рекурсивных функций, формальных систем. Математическая логика находит приложение в электротехнике (исследование релейно-контактных и электронных схем), вычислительной технике (программирование), кибернетике (теория автоматов), нейрофизиологии (моделирование нейронных сетей), языкознании (структурная лингвистика и семиотика). | ||
| + | |||
| + | Еще мы нашли информацию по нечеткой логике(Fuzzy logic): | ||
| + | [http://http://ru.wikipedia.org/wiki/Fuzzy_Logic Нечеткая логика] и теория нечётких множеств — раздел математики, являющийся обобщением классической логики и теории множеств. Понятие нечёткой логики было впервые введено профессором Лютфи Заде в 1965 году. В этой статье понятие множества было расширено допущением, что функция принадлежности элемента к множеству может принимать любые значения в интервале [0...1], а не только 0 или 1. Такие множества были названы нечёткими. Также автором были предложены различные логические операции над нечёткими множествами и предложено понятие лингвистической переменной, в качестве значений которой выступают нечёткие множества. | ||
<center>'''Нами была создана карта знаний по основным логическим элементам'''</center> | <center>'''Нами была создана карта знаний по основным логическим элементам'''</center> | ||
| Строка 53: | Строка 55: | ||
<center> | <center> | ||
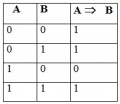
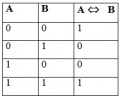
| + | '''Таблицы истинности''' | ||
<gallery> | <gallery> | ||
Изображение:Screenshot-3.jpg|КОНЪЮНКЦИЯ (логическое умножение) | Изображение:Screenshot-3.jpg|КОНЪЮНКЦИЯ (логическое умножение) | ||
| Строка 62: | Строка 65: | ||
</center> | </center> | ||
| − | + | ||
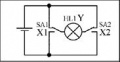
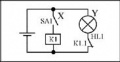
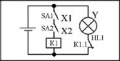
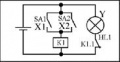
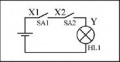
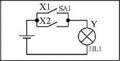
<center>'''Примеры релейно-контактных схем'''</center> | <center>'''Примеры релейно-контактных схем'''</center> | ||
| Строка 76: | Строка 79: | ||
</gallery> | </gallery> | ||
</center> | </center> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
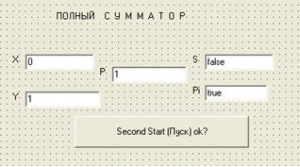
'''[http://ru.wikipedia.org/wiki/Полусумматор Полусумматор]'''— логическая схема имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Полусумматор используется для построения двоичных сумматоров. Полусумматор позволяет вычислять сумму A+B, где A и B — это разряды двоичного числа, при этом результатом будут два бита S,C, где S — это бит суммы по модулю, а C — бит переноса. | '''[http://ru.wikipedia.org/wiki/Полусумматор Полусумматор]'''— логическая схема имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Полусумматор используется для построения двоичных сумматоров. Полусумматор позволяет вычислять сумму A+B, где A и B — это разряды двоичного числа, при этом результатом будут два бита S,C, где S — это бит суммы по модулю, а C — бит переноса. | ||
Версия 12:51, 26 октября 2010
СодержаниеНазвание проектаУчебный проект Вычисляем рассуждения Авторы и участники проекта
Тема исследования группыПриложения математической логики в современной электронно-вычислительной технике. Поставленные задачи1) Создать группу <<Инженеры>> на Google для организации взаимодействия в
ходе исследовательской работы. Проблемный вопрос (вопрос для исследования)Как аппарат математической логики применяется в современной электронно-вычислительной технике? Гипотеза исследованияМы предполагаем, что математическая логика Цели исследованияПровести анализ возможностей использования языка математической логики в современной электронно-вычислительной технике. Результаты исследованияНами была создана Google группа Был произведён подбор ссылок на сервисе ДоброгоБобра Математическая логика (или символическая логика) - область знания, которая сложилась в результате применения в логике формальных методов математики и логического исследования математических рассуждений и доказательств. В математической логике логические процессы изучаются посредством их отображения в формализованных языках, или логических исчислениях. Наряду с изучением формального строения логических исчислений (Логический синтаксис) в математической логике встает также задача рассмотрения отношений между исчислениями и теми содержательными областями, которые служат их интерпретациями и моделями. Эта задача обрисовывает проблематику логической семантики. Логический синтаксис и семантика включаются в металогику - теорию средств описания, предпосылок и свойств логических исчислений. Некоторые исходные понятия математической логике содержатся уже в учении мегаро-стоической школы (3 в. до н. э.). Саму же идею логического исчисления, по-видимому, впервые сформулировал Лейбниц. Однако как самостоятельная дисциплина математическая логика оформилась в середине 19 в. благодаря работам Буля. С Буля начинается развитие так называемой алгебры логики. Другое направление разработки математической логики ставшее определяющим, начинается с конца 19 века в связи с потребностями математики в обосновании своих понятий и способов доказательств. У истоков этого направления лежат труды Фреге. Значительный вклад в его развитие внесли Рассел, Уайтхед и Гильберт. В этот период создаются фундаментальные логические системы математической логики - классические исчисление высказываний и исчисление предикатов. Крупные результаты, определившие современное состояние математической логики, были получены в. 30-х гг. Гёделем. Тарским, А. Чёрчем. Современный этап математической логики характеризуется исследованием разнообразных видов логических исчислений, интересом к проблемам семантики и вообще металогики, к вопросам специальных математических и технических приложений логики. В связи с задачами обоснования математики наряду с работами в области классической математической логике разрабатывается интуиционистская и конструктивная логика. С анализом оснований логики связаны исследования по комбинаторной логике. Ведутся исследования в области многозначных, модальных и релевантных логик. Математическая логика оказала влияние на развитие ряда разделов современной математики, общей алгебры, теории алгоритмов, рекурсивных функций, формальных систем. Математическая логика находит приложение в электротехнике (исследование релейно-контактных и электронных схем), вычислительной технике (программирование), кибернетике (теория автоматов), нейрофизиологии (моделирование нейронных сетей), языкознании (структурная лингвистика и семиотика). Еще мы нашли информацию по нечеткой логике(Fuzzy logic): Нечеткая логика и теория нечётких множеств — раздел математики, являющийся обобщением классической логики и теории множеств. Понятие нечёткой логики было впервые введено профессором Лютфи Заде в 1965 году. В этой статье понятие множества было расширено допущением, что функция принадлежности элемента к множеству может принимать любые значения в интервале [0...1], а не только 0 или 1. Такие множества были названы нечёткими. Также автором были предложены различные логические операции над нечёткими множествами и предложено понятие лингвистической переменной, в качестве значений которой выступают нечёткие множества. 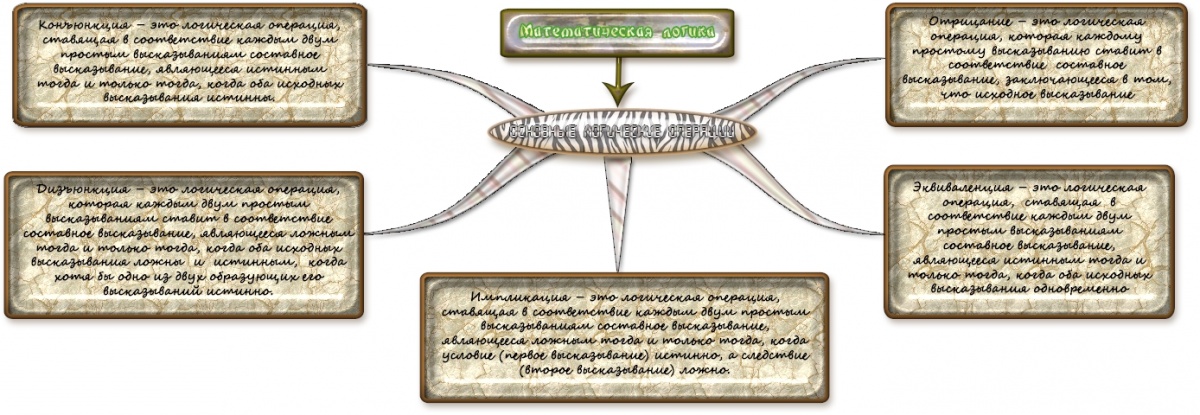 Таблицы истинности
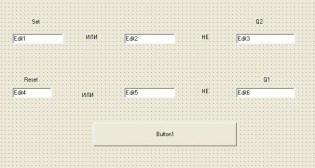
Полусумматор— логическая схема имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Полусумматор используется для построения двоичных сумматоров. Полусумматор позволяет вычислять сумму A+B, где A и B — это разряды двоичного числа, при этом результатом будут два бита S,C, где S — это бит суммы по модулю, а C — бит переноса. Сумматор — логический операционный узел, выполняющий арифметическое сложение двоичных, троичных или n-ичных кодов двух (бинарный), трёх (тринарный) или n чисел (n-нарный). При арифметическом сложении выполняются и другие дополнительные операции: учёт знаков чисел, выравнивание порядков слагаемых и тому подобное. Триггер — класс электронных устройств, обладающих способностью длительно находиться в одном из двух или более устойчивых состояний и чередовать их под воздействием внешних сигналов. Каждое состояние триггера легко распознаётся по значению выходного напряжения. По характеру действия триггеры относятся к импульсным устройствам — их активные элементы (транзисторы, лампы) работают в ключевом режиме, а смена состояний длится очень короткое время.
ВыводВ ходе проектной деятельности мы выяснили роль логических элементов в вычислительной технике. Для классификации логических элементов нами построен кластер. Выполнено моделирование на языке Delphi триггера, полу сумматора и сумматора. Выполнен подбор ссылок по теме проекта, создана карта знаний демонстрирующая основные логические элементы. Полезные ресурсыАлгебра логики и логические основы компьютера Методическое пособие по информатике Круподёровой Елены Петровны |
||||||||||