Результаты исследований группы Инженеры в проекте Вычисляем рассуждения

Название проекта

Учебный проект Вычисляем рассуждения

Авторы и участники проекта

1. Плеханов Семён Петрович
2. Лабзин Андрей Федорович
3. Гришин Евгений Анатольевич
4. Кислицкий Илья Станиславович
5. Комаров Иван Александрович

Тема исследования группы

Как аппарат математической логики применяется в современной электронно-вычислительной технике?

Поставленные задачи

1) Создать группу <<Инженеры>> на Google для организации взаимодействия в ходе исследовательской работы.
2) Осуществить совместный подбор ссылок на Интернет-ресурсы и поиск информации в печатных изданиях по теме исследования.
3) Провести анализ полученной информации по теме исследования и ответить на вопросы:
а) как язык классической математической логики находит применение при построении релейно-контактных схем?
б) что такое нечеткая логика и в каких областях она применяется?
4) Сформулировать выводы по результатам исследования.
5) Оформить результаты исследования.

Проблемный вопрос (вопрос для исследования)

Как происходит взаимодействие логической части программы с её физической начинкой.

Гипотеза исследования

Проанализировать возможности языка математической логики в современной электронно-вычислительной технике.
Как используются в технике :

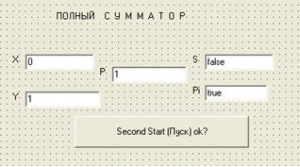
• Полусумматор.
  
• Сумматор.
  
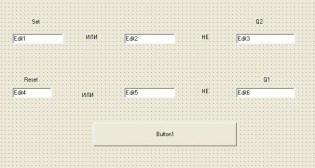
• Триггер.
  

Цели исследования

Провести анализ возможностей использования языка математической логики в современной электронно-вычислительной технике.

Результаты исследования

Применение в логике математических методов становится возможным тогда, когда суждения формулируются на некотором точном языке. Такие точные языки имеют две стороны: синтаксис и семантику. Синтаксисом называется совокупность правил построения объектов языка (обычно называемых формулами). Семантикой называется совокупность соглашений, описывающих наше понимание формул (или некоторых из них) и позволяющих считать одни формулы верными, а другие — нет.
Важную роль в математической логике играют понятия дедуктивной теории и исчисления. Исчислением называется совокупность правил вывода, позволяющих считать некоторые формулы выводимыми. Правила вывода подразделяются на два класса. Одни из них непосредственно квалифицируют некоторые формулы как выводимые. Такие правила вывода принято называть аксиомами. Другие же позволяют считать выводимыми формулы A, синтаксически связанные некоторым заранее определённым способом с конечными наборами A1,....An выводимых формул. Широко применяемым правилом второго типа является правило modus ponens: если выводимы формулы A и (А->B), то выводима и формула B.
Отношение исчислений к семантике выражается понятиями семантической пригодности и семантической полноты исчисления. Исчисление И называется семантически пригодным для языка Я, если любая выводимая в И формула языка Я является верной. Аналогично, исчисление И называется семантически полным в языке Я, если любая верная формула языка Я выводима в И.Математическая логика изучает логические связи и отношения лежащие в основе логического ( дедуктивного ) вывода с использованием языка математики.
Многие из рассматриваемых в математической логике языков обладают семантически полными и семантически пригодными исчислениями. В частности, известен результат К. Гёделя о том, что так называемое классическое исчисление предикатов является семантически полным и семантически пригодным для языка классической логики предикатов первого порядка. С другой стороны, имеется немало языков, для которых построение семантически полного и семантически пригодного исчисления невозможно. В этой области классическим результатом является теорема Гёделя о неполноте, утверждающая невозможность семантически полного и семантически пригодного исчисления для языка формальной арифметики.
Стоит отметить, что на практике множество элементарных логических операций является обязательной частью набора инструкций всех современных микропроцессоров и соответственно входит в языки программирования. Это является одним из важнейших практических приложений методов математической логики, изучаемых в современных учебниках информатики.

Полусумматор	Полный сумматор	Тригер
var x,y,Pi,P,S:Boolean; procedure TForm1.Button1Click(Sender: TObject); begin x:=strtobool(edit5.text); y:=strtobool(edit6.text); Pi:=strtobool(edit7.text); P:=(not x and y and Pi)or(x and not y and Pi)or(x and y and not Pi)or(x and y and Pi); S:=(not x and not y and Pi)or(not x and y and not Pi)or(x and not y and not Pi)or(x and y and Pi); edit8.text:=booltostr(S,true); edit9.text:=booltostr(P,true); end; end.	var x,y,s,p,pi :boolean; procedure TForm1.Button1Click(Sender: TObject); begin x:=strtobool(edit5.Text); y:=strtobool(edit6.Text); p:=strtobool(edit7.Text); s:=(not x and not y and p) or (not x and y and not p) or (x and not y and not p) or (x and y and p); pi:=(not x and y and p) or (x and not y and p) or(x and y and not p) or(x and y and p); edit8.text:=booltostr(s,true); edit9.text:=booltostr(pi,true); end; end.	var S,R,Or1Out,Not1out,or2out,not2out:boolean procedure TForm2.Button1Click(Sender: TObject); begin S:=StrToBool(editset.text); R:=StrToBool(editreset.text); or1out:=s or not2out; not1out:=not or1out; or2out:=not1 out or r; not2out:=bot or2out; editor1out.text:=booltostr(or1out,true); editor2out.text:=booltostr(or2out,true); editq2.text:=booltostr(not1out,true); editq1.text:=booltostr(not2out,true); end; end.

Полезные ресурсы

Математическая логика

Сетунь(компьютер)

Логика в информатике

Алгебра логики и логические основы компьютера

Полусумматор

Сумматор

Триггер