Результаты исследований группы Инженеры в проекте Вычисляем рассуждения

Название проекта

Учебный проект Вычисляем рассуждения

Авторы и участники проекта

1. Плеханов Семён Петрович
2. Лабзин Андрей Федорович
3. Гришин Евгений Анатольевич
4. Кислицкий Илья Станиславович
5. Комаров Иван

Тема исследования группы

Как аппарат математической логики применяется в современной электронно-вычислительной технике?

Поставленные задачи

1) Создать группу <<Инженеры>> на Google для организации взаимодействия в ходе исследовательской работы.
2) Осуществить совместный подбор ссылок на Интернет-ресурсы и поиск информации в печатных изданиях по теме исследования.
3) Провести анализ полученной информации по теме исследования и ответить на вопросы:
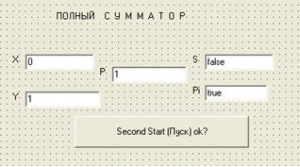
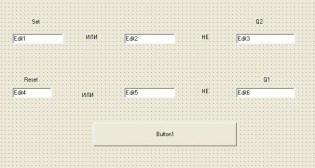
а) как язык классической математической логики находит применение при построении релейно-контактных схем?
б) что такое нечеткая логика и в каких областях она применяется?
4) Сформулировать выводы по результатам исследования.
5) Оформить результаты исследования.

Цели исследования

Провести анализ возможностей использования языка математической логики в современной электронно-вычислительной технике.

Результаты исследования

Полусумматор	Полный сумматор	Тригер
var x,y,Pi,P,S:Boolean; procedure TForm1.Button1Click(Sender: TObject); begin x:=strtobool(edit5.text); y:=strtobool(edit6.text); Pi:=strtobool(edit7.text); P:=(not x and y and Pi)or(x and not y and Pi)or(x and y and not Pi)or(x and y and Pi); S:=(not x and not y and Pi)or(not x and y and not Pi)or(x and not y and not Pi)or(x and y and Pi); edit8.text:=booltostr(S,true); edit9.text:=booltostr(P,true); end; end.	var x,y,s,p,pi :boolean; procedure TForm1.Button1Click(Sender: TObject); begin x:=strtobool(edit5.Text); y:=strtobool(edit6.Text); p:=strtobool(edit7.Text); s:=(not x and not y and p) or (not x and y and not p) or (x and not y and not p) or (x and y and p); pi:=(not x and y and p) or (x and not y and p) or(x and y and not p) or(x and y and p); edit8.text:=booltostr(s,true); edit9.text:=booltostr(pi,true); end; end.	var S,R,Or1Out,Not1out,or2out,not2out:boolean procedure TForm2.Button1Click(Sender: TObject); begin S:=StrToBool(editset.text); R:=StrToBool(editreset.text); or1out:=s or not2out; not1out:=not or1out; or2out:=not1 out or r; not2out:=bot or2out; editor1out.text:=booltostr(or1out,true); editor2out.text:=booltostr(or2out,true); editq2.text:=booltostr(not1out,true); editq1.text:=booltostr(not2out,true); end; end.

Полезные ресурсы

Математическая логика

Сетунь(компьютер)

Логика в информатике

Алгебра логики и логические основы компьютера

Полусумматор

Сумматор

Триггер