Результаты исследования учащихся в проекте Божественная пропорция
Содержание
Авторы и участники проекта
- Кучерова Елена
- Участники группы "Архитекторы"
Тема исследования группы
Золотое сечение в архитектуре
Проблемный вопрос (вопрос для исследования)
Как применяется золотое сечение в архитектуре?
Гипотеза исследования
Мы считаем, что наиболее совершенные архитектурные сооружения созданы на основе золотого сечения.
Цели исследования
- выявить источники совершенства архитектурной формы;
- выяснить связь божественной пропорции с архитектурой;
- рассмотреть некоторые архитектурные памятники, построенные по золотому сечению;
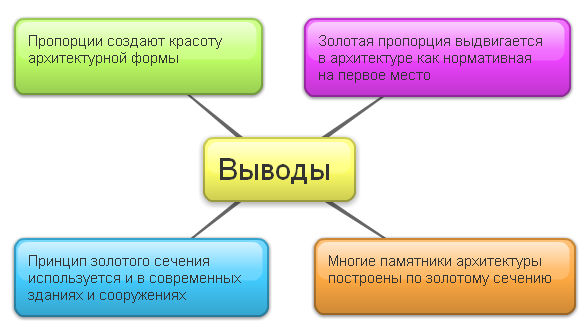
- проверить использование принципа золотого сечения в современных зданиях и сооружениях;
- подготовить коллекцию фотографий с историческими и современными архитектурными зданиями и сооружениями;
Результаты проведённого исследования
В ходе исследования было выяснено следующее:
Главная ценность архитектурных сооружений в их красоте. Сооружение может быть прочным и удобным, но если оно не привлекает глаз, не вызывает у нас эстетического чувства, то оно воспринимается нами как обычное строение, но не как памятник архитектуры. Другими словами, без искусства архитектуры нет. Существуют конкретные математические модели, соотношения и свойства, которые используются в архитектуре и определяют их эстетическое совершенство. Это разнообразные геометрические формы, пропорции и законы симметрии, которые в определенной мере задают внутреннюю красоту архитектурной формы. Без нее внешние украшения зданий не улучшают, а порой усугубляют внешнее впечатление о том или ином сооружении.
Обратимся к высказываниям людей, которые не только оставили значительный след в архитектуре, но и пытались понять источники совершенства архитектурной формы.
Французский зодчий, живший в XVII веке, Франсуа Блондель [1] писал: «Удовлетворение, которое мы испытываем, глядя на прекрасное произведение искусства, проистекает от того, что в нем соблюдены правила и мера, ибо удовольствия в нас вызывают единственно лишь пропорции. …Дабы подкрепить наше утверждение, я заявляю, что красота, возникающая из меры и пропорции, вовсе не требует дорогих материалов и изящной работы, дабы вызвать восхищение, напротив, она сверкает и делается все ощутимее, проступая сквозь грязь и хаос материала и его обработки». Лучшим подтверждением этих слов является скромная, не отличающаяся значительными размерами церковь Покрова Богородицы на Нерли. Но именно связь размеров (соразмерность) всех ее частей создает ту гармонию, которая делает ее прекрасной.
Другое высказывание принадлежит выдающемуся русскому архитектору XIX-XX веков, автору Мавзолея В. И.Ленина на Красной площади, Казанского вокзала, здания гостиницы «Москва» А. В.Щусеву [2]: «Пожалуй, самым трудным и вместе с тем обязательным в архитектурном творчестве является простота. Простота форм обязывает придавать прекрасные пропорции и соотношения, которые сообщили бы им необходимую гармонию».
Именно гармония, которая лежит в основе всех искусств, обусловливает красоту их лучших образцов. Но, чтобы создать рукотворные произведения архитектуры, нужно познать и использовать законы гармонии при их создании. А вот раскрыть эти законы гармонии как раз и помогает математика.
Человечество с самых ранних этапов своего существования пыталось постичь разумом законы гармонии, а значит, красоты. И одними из первых совершили открытие связи прекрасного и математики представители школы пифагорийцев. Известен их девиз «Все прекрасное, благодаря числу». Ведь именно число позволило найти меру вещей, а значит соотнести, соразмерить различные части целого. Наиболее ярко это видно в лучших произведениях архитектуры Древней Греции.
Вслед за пифагорийцами Аристотель пытался найти сущность красоты. Он писал в своей знаменитой работе «Метафизика»: «… важнейшие виды прекрасного – это слаженность, соразмерность и определенность, математика больше всего и выявляет именно их».
Математика предлагает архитектору ряд, если так можно назвать, общих правил организации частей в целое, которые помогают расположить эти части в пространстве так, что в них проявлялся порядок, установить определенное соотношение между размерами частей и задать для изменения размеров (уменьшения или увеличения) определенную единую закономерность, что обеспечивает восприятие целостности и представление о порядке;
выделить определенное место в пространстве, где будет размещаться сооружение, описать его определенной математической формой, которая также позволит выделить его из других сооружений и внести в их состав, создав новую композицию, новый архитектурный ансамбль.
«Ввиду исключительного значения золотого сечения [3] в смысле такого пропорционального деления, которое устанавливает постоянную связь между целым и его частями, и дает постоянное между ними соотношение, недостигаемое никаким другим делением, схема, основанная на нем, выдвигается как нормативная на первое место и принята как при проверке основ пропорциональности исторических памятников, так и современных сооружений…
Считаясь с этим общим значением золотого сечения во всех проявлениях архитектурной мысли, теорию пропорциональности, основанную на делении целого на пропорциональные части, отвечающие членам геометрической прогрессии золотого сечения, следует признать основой архитектурной пропорциональности вообще».
Так говорится о золотом сечении в хорошо известной в теории архитектуры книге «Пропорциональность в архитектуре», опубликованной русским архитектором профессором Г.Д. Гриммом [4] в 1935 г.
Проведенные им исследования приводят к заключению, что для полной пропорциональной согласованности архитектурного памятника, представляющего собой во всяком случае объемное решение, требуется пропорциональное согласование прежде всего его линейных размеров по высотам и горизонталям, следствием чего и является пропорциональное решение фасадных площадей и далее всего объема».
Анализ литературы и Интернет-источников по теме исследования позволил выяснить, какие памятники архитектуры построены по золотому сечению.
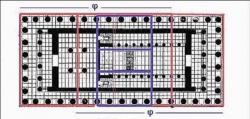
ПАРФЕНОН
Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.). Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по “золотому сечению”, то получим те или иные выступы фасада. Говорят «… у греческого храма нет размеров, у него есть пропорции …».
На рисунке виден целый ряд закономерностей, связанных с золотым сечением. Пропорции здания можно выразить через различные степени числа Ф=0,618...
На плане пола Парфенона также можно заметить "золотые прямоугольники".
ПАНТЕОН
Другим примером из архитектуры древности является Пантеон.
НОТР-ДАМ ДЕ ПАРИ
Золотое соотношение мы можем увидеть и в здании собора Парижской Богоматери (Нотр-дам де Пари)
ХРАМ ВАСИЛИЯ БЛАЖЕННОГО
Пропорции Покровского собора на Красной площади в Москве (более известного как храм Василия Блаженного) определяются восемью членами ряда золотого сечения: 1, φ, φ2 … φ7. Многие члены этого ряда повторяются в затейливых элементах храма многократно, причем φ + φ2 = 1, φ2 + φ3 = φ, φ3 + φ4 = φ2, φ4 + φ5 =φ3 и т. д.
Золотое сечение в современных зданиях и сооружениях.
Проект небоскреба на Лубянской площади в Москве. Пропорции. В.Кринский
Отношениям золотого ряда следуют формы клуба на Лесной улице (пример - низ углового стеклянного цилиндра и лежащий на нем прямоугольный объем).
Здание клуба на Лесной улице в Москве. И.Голосов "Золото" - торцы боковых объемов и просвет меж ними в известном проекте "Оргаметалла".
Проект здания "Оргаметалла" в Москве. М.Гинзбург
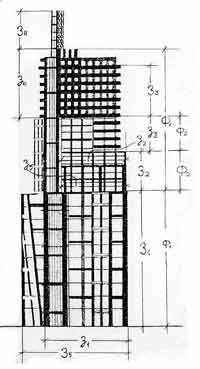
Мавзолей вобрал в себя весь спектр золотых отношений...
Мавзолей. Пропорции. А.Щусев
Выводы
Выводы оформлены с помощью сервиса bubbl.us
Полезные ресурсы
Пропорциональность в архитектуре