Результаты исследований обучающихся в проекте Методы координат с другого ракурса
Содержание
Авторы и участники проекта
Участники группы: "Следопыты"
Тема исследования группы
Метод координат в повседневной жизни
Проблемный вопрос (вопрос для исследования)
Где встречается метод координат в повседневной жизни?
Гипотеза исследования
Мы считаем, что метод координат используется во многих областях нашей повседневной жизни
Цели исследования
1. Изучить дополнительную литературу по теме исследования
2.Рассмотреть и проанализировать области применения метода координат
3.Провести опрос одноклассников об использовании метода координат в повседневной жизни
4.Проанализировать полученные результаты, определить достигнуты ли цели
Результаты проведённого исследования
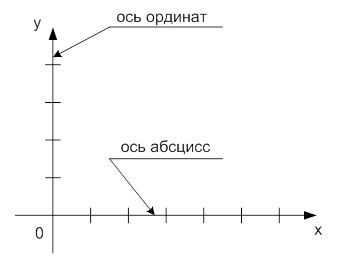
Изучив дополнительную литературу , мы выявили способы использования координатной плоскости в математике. Чтобы из обычной плоскости получить координатную, необходимо начертить две перпендикулярные прямые, отмечая стрелками направления «вправо» и «вверх»(Рис.1). На прямые наносят деления, как на линейку, причем точка пересечения прямых – это нулевая отметка для обеих шкал. Горизонтальную прямую обозначают и называют осью абсцисс, вертикальную прямую обозначают и называют осью ординат.
Мы рассмотрели и проанализировали области применения системы координат в повседневной жизни, и выяснили, с координатами в жизни мы сталкиваемся постоянно, можно сказать «на каждом шагу». Идея задавать положение точки на плоскости с помощью чисел зародилась в древности — прежде всего у астрономов и географов при составлении звездных и географических карт, календаря.
Подробное изучение координатной плоскости необходимо, ведь координаты- это тот же адрес. Система координат - это правило, по которому определяется положение того или иного объекта. Метод координат позволяет применять средства алгебры и математического анализа при решении геометрических задач. При работе с координатной плоскостью мы неоднократно можем менять расположение точек, размеры единичных отрезков, что требует высокого развития и логического мышления, и, следовательно, способствует его развитию. Мы выяснили, что в окружающем нас мире существует много явлений и объектов-прообразов, которые можно использовать для составления заданий на метод координат. Если на уроках математики, каждой точке на числовой прямой ставилась в соответствии единственная координата (единственный адрес), то на уроках географии каждой точке на карте соответствуют уже два адреса, две координаты – долгота и широта. Так, значит, существует взаимосвязь между математическими координатами и географическими координатами. Весьма интересный материал предоставляет нам астрономия, где каждое созвездие тесно связанно с координатами.
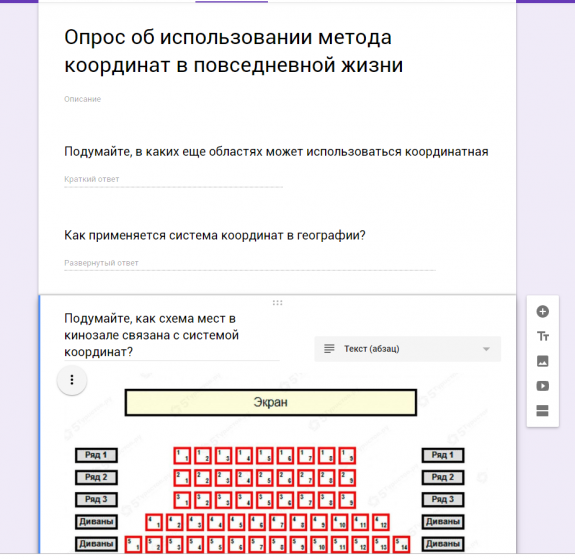
На системе координат основаны многие способы указания места. Например,на билете в кинотеатр стоят два числа: ряд и место — их можно рассматривать как координаты места в зале. Подобные координаты приняты о шахматах. Вместо одного из чисел берется буква: вертикальные ряды клеток обозначаются буквами латинского алфавита, а горизонтальные — цифрами. Таким образом, каждой клетке шахматной доски ставится в соответствие буква и число, и шахматисты получают возможность записывать свои партии. Также эта система используется и в поездах, что бы найти своё место в поезде. Об этом рассуждал А. Савин в статье "Координаты" в научно-популярном журнале "Квант". Так же, как и каждый дом имеет свой адрес (с названием улицы, города), также и каждое место на поверхности Земли можно записать в виде адреса, используя линию широты (параллель) и линию долготы (меридиан), проходящие через это место. Чтобы найти некоторый объект в городе, в большинстве случаев достаточно знать его адрес. Трудности возникают, если нужно объяснить, где находится, например, дачный участок, место в лесу. Универсальным средством указания местоположения служат географические координаты.
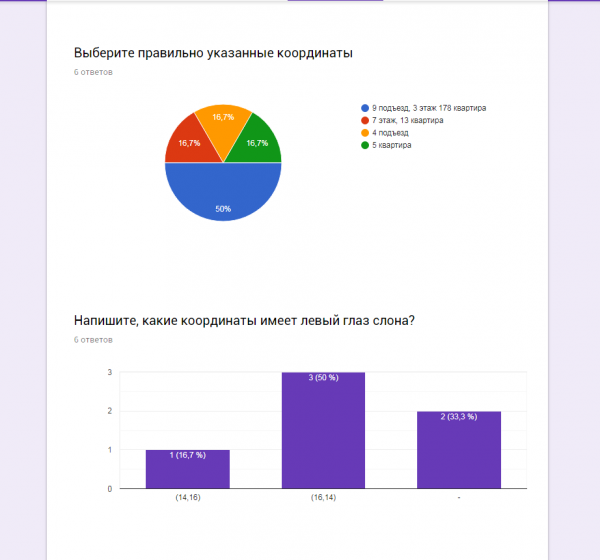
Среди одноклассников мы провели опрос и выявили, что они недостаточно хорошо знают способы использования координатной плоскости в повседневной жизни.
3-4 абзаца текста таблциы, ментальные карты, ленты времени (хотя бы 2 сервиса)
Вывод
Полезные ресурсы
Савин А.А. Координаты // Квант. 1977. №9