Результаты исследования учащихся в проекте безработица

Авторы и участники проекта

1. Новбатов Азат

Тема исследования группы

Каковы последствия безработицы?

Проблемный вопрос (вопрос для исследования)

1)Как используется математическое и компьютерное моделирование в математике?

Цели исследования

1)Проанализировать математическое и компьютерное моделирование в математике.

2)Привести примеры математического моделирования.

3)Применение математического моделирования.

Результаты проведённого исследования

При математизации научных знаний выделяется этап абстрагирования от конкретной природы явления, идеализации и выделения его математической формы (строится математическая модель). Именно абстрактность математической модели порождает определенные трудности для ее применения к описанию конкретного явления или процесса. Сейчас, благодаря накопленному опыту, процесс идеализации, абстрагирования проходит значительно спокойнее и быстрее в различных науках.

Вторым этапом математизации является исследование математических моделей как чисто математических (абстрактных) объектов. С этой целью используются средства самой математики как уже созданные, так и специально построенные. В настоящее время большие возможности для исследования математических моделей предоставляют вычислительные средства: компьютеры и численные методы.

Третий этап применения математики в прикладных исследованиях характеризуется интерпретацией - приданием конкретного прикладного содержания математическим абстракциям. Специалист по прикладному математическому моделированию, работая бок о бок со специалистами в прикладной области, всегда за математическими абстракциями видит конкретное прикладное содержание.

Математические модели могут изучаться в традициях чистой математики. В этом случае математические модели изучаются сами по себе, без какой-либо связи с прикладным содержанием. Они исследуются на принятом в математике уровне строгости, что обеспечивает им универсализм и необходимую общность.

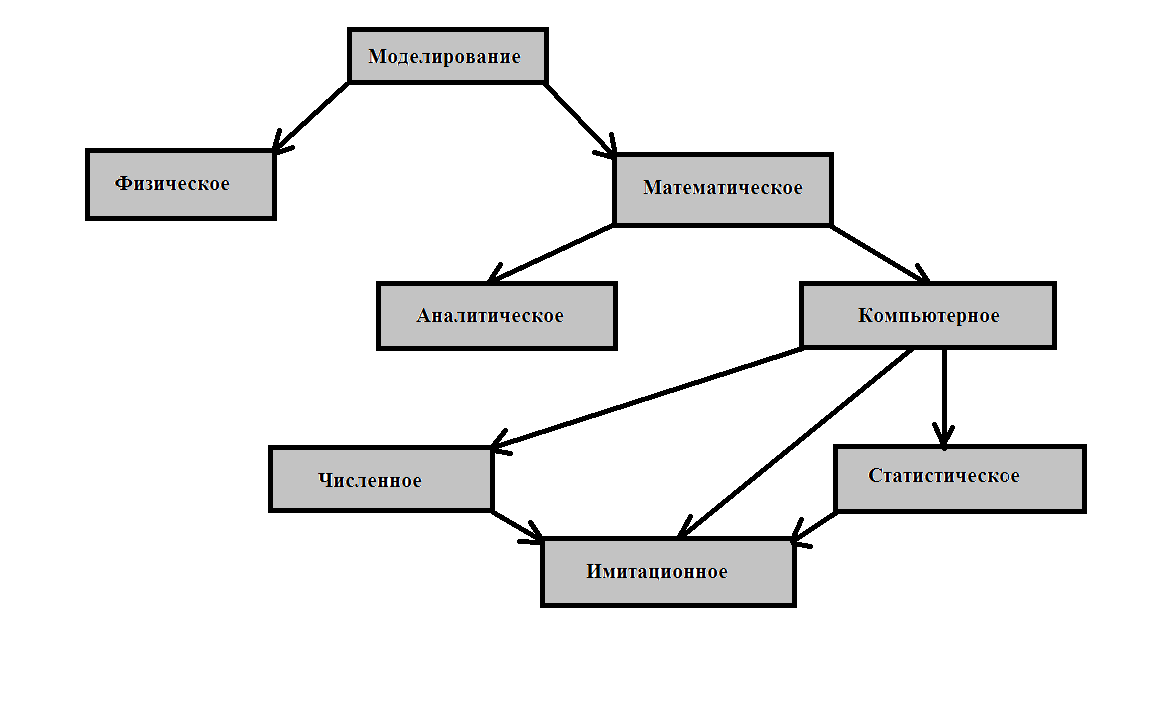
Классификация видов моделирования:

Вывод

Проанализировали компьютерное и математическое моделирование, привели примеры, и построили классификацию математического моделирования, выделили три этапа математического моделирования.

Полезные ресурсы

Математическое и компьютерное моделирование:[[1]]

Краткая информация о математическом моделировании: [[2]]