Результаты исследований учащихся в проекте Связанные одной сетью

Авторы и участники проекта

• Барсук Наталья

• Участники группы историки

Тема исследования группы

История создания и развития сети Интернет

Проблемный вопрос (вопрос для исследования)

Какова история развития Интернета?

Гипотеза исследования

Какими способами можно решать логические задачи?

Цели исследования

- Разработать презентацию

- Осуществить совместный подбор ссылок на Интернет-ресурсы и поиск информации в печатных изданиях по теме исследования.

- Осуществить анализ основных методов решения логических задач .

- Сформулировать выводы по результатам исследования.

- Оформить результаты исследования.

- Защитить проект.

Результаты проведённого исследования

Алгебра в широком смысле этого слова — наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над разнообразными математическими объектами. Многие математические объекты (целые и рациональные числа, многочлены, векторы, множества) вы изучаете в школьном курсе алгебры, где знакомитесь с такими разделами математики, как алгебра чисел, алгебра многочленов, алгебра множеств и т. д.

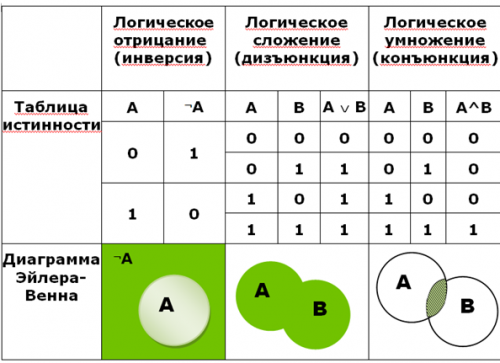
Для информатики важен раздел математики, называемый алгеброй логики; объектами алгебры логики являются высказывания.

• Высказывание — это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.

Обоснование истинности или ложности высказываний решается теми науками, к сфере которых они относятся. Алгебра логики отвлекается от смысловой содержательности высказываний. Её интересует только то, истинно или ложно данное высказывание. В алгебре логики высказывания обозначают буквами и называют логическими переменными. При этом если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей (А = 1), а если ложно — нулём (В = 0). 0 и 1, обозначающие значения логических переменных, называются логическими значениями.

Алгебра логики определяет правила записи, вычисления значений, упрощения и преобразования высказываний.

Рассмотрим два высказывания: А = «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу», В = «Лейбниц является основоположником бинарной арифметики». Очевидно, новое высказывание «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу или Лейбниц является основоположником бинарной арифметики» ложно только в том случае, когда одновременно ложны оба исходных высказывания.

• Дизъюнкция — логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.

• Инверсия — логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.

• Конъюнкция — логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Более подробно тему алгебры-логики мы раскрыли с помощью презентации Логические элементы

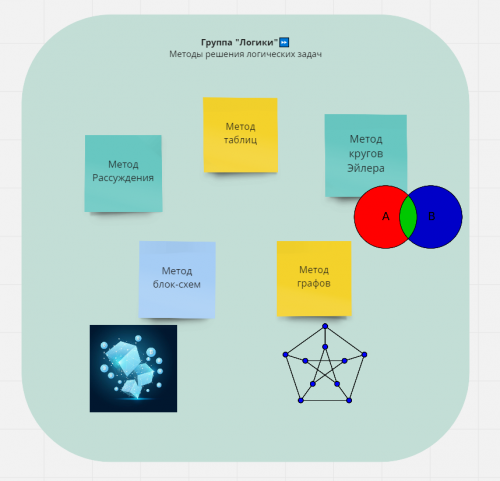
Так же мы рассмотрели различные способы решения задач, результаты исследования отразили на онлайн-доске Методы решения логических задач

Вывод

В результате работы над исследованием мы пришли к выводу, что способы решения логических задач очень разнообразны,при выборе того или иного способа решения нужно исходить из особенностей поставленной задачи.

Полезные ресурсы

• Примеры логических задач

• Математическая логика

Другие документы

Учебный проект Исследуем математические основы информатики