Результаты исследований обучающихся в проекте Квадратные уравнения: различия между версиями
(→Результаты проведённого исследования) |
(→Результаты проведённого исследования) |
||
| Строка 40: | Строка 40: | ||
6.Решение уравнений с использованием теоремы Безу. | 6.Решение уравнений с использованием теоремы Безу. | ||
| − | Наиболее интересными оказались следующие методы:свойство коэффициентов квадратного уравнения | + | Наиболее интересными оказались следующие методы:свойство коэффициентов квадратного уравнения; геометрический способ решения квадратных уравнений и применение Теоремы Безу. |
| − | Рассмотрим метод | + | Рассмотрим метод,основанный на свойстве коэффициентов квадратного уравнения. |
Пусть дано квадратное уравнение ах2 + bх + с = 0, а ≠ 0. 1. Если a+ b + с = 0 (т.е. сумма коэффициентов уравнения равна нулю), то х1 = 1. 2. Если а - b + с = 0, или b = а + с, то х1 = - 1. | Пусть дано квадратное уравнение ах2 + bх + с = 0, а ≠ 0. 1. Если a+ b + с = 0 (т.е. сумма коэффициентов уравнения равна нулю), то х1 = 1. 2. Если а - b + с = 0, или b = а + с, то х1 = - 1. | ||
| Строка 52: | Строка 52: | ||
Существуют и другие свойства коэффициентов квадратного уравнения. но их использование более сложное. | Существуют и другие свойства коэффициентов квадратного уравнения. но их использование более сложное. | ||
| − | + | Рассмотрим геометрический способ решения квадратных уравнений. | |
Пример. | Пример. | ||
| Строка 77: | Строка 77: | ||
Для искомой стороны х первоначального квадрата получим x=8-2,5-2,5=3. | Для искомой стороны х первоначального квадрата получим x=8-2,5-2,5=3. | ||
| + | |||
| + | Рассмотрим решение квадратных уравнений при помощи теоремы Безу. | ||
| + | |||
| + | Остаток от деления многочлена P(x) на двучлен x - α равен P(α) (т.е. значению P(x) при x = α). Если число α является корнем многочлена P(x), | ||
| + | |||
| + | то этот многочлен делится на x -α без остатка. Пример.х²-4х+3=0 Р(x)= х²-4х+3, α: ±1,±3, α =1, 1-4+3=0. | ||
| + | |||
| + | Разделим Р(x) на (х-1):(х²-4х+3)/(х-1)=х-3 х²-4х+3=(х-1)(х-3), (х-1)(х-3)=0 х-1=0; х=1, или х-3=0, х=3; Ответ: х1=2, х2=3. | ||
| + | |||
| + | Вывод: Умение быстро и рационально решать квадратные уравнения просто необходимо для решения более сложных уравнений, | ||
| + | |||
| + | например, дробно-рациональных уравнений, уравнений высших степеней, биквадратных уравнений, а в старшей школе тригонометрических, | ||
| + | |||
| + | показательных и логарифмических уравнений. Изучив все найденные способы решения квадратных уравнений, | ||
| + | |||
| + | мы можем посоветовать одноклассникам, кроме стандартных способов, решение способом переброски (6) и решение | ||
| + | |||
| + | уравнений по свойству коэффициентов (7), так как они являются более доступными для понимания. | ||
==Вывод== | ==Вывод== | ||
Версия 17:47, 24 сентября 2018
Содержание
Авторы и участники проекта
Участники группы: Гении
Тема исследования группы
Необычные методы решения квадратных уравнений.
Проблемный вопрос (вопрос для исследования)
Какие необычные методы решения квадратных уравнений существуют?
Цели исследования
- Проанализировать все известные методы решения квадратных уравнений.
- Выявить самые необычные и интересные методы решения уравнений.
- Привести примеры применения найденных методов на практике.
Результаты проведённого исследования
1.Стандартные способы решения квадратных уравнений из школьной программы:
а)Разложение левой части уравнения на множители.
б)Метод выделения полного квадрата.
в)Решение квадратных уравнений по формуле.
г)Графическое решение квадратного уравнения.
д)Решение уравнений с использованием теоремы Виета.
2.Решение уравнений способом "переброски".
3.Свойства коэффициентов квадратного уравнения.
4.Решение квадратных уравнений с помощью номограммы.
5.Геометрический способ решения квадратных уравнений.
6.Решение уравнений с использованием теоремы Безу.
Наиболее интересными оказались следующие методы:свойство коэффициентов квадратного уравнения; геометрический способ решения квадратных уравнений и применение Теоремы Безу.
Рассмотрим метод,основанный на свойстве коэффициентов квадратного уравнения.
Пусть дано квадратное уравнение ах2 + bх + с = 0, а ≠ 0. 1. Если a+ b + с = 0 (т.е. сумма коэффициентов уравнения равна нулю), то х1 = 1. 2. Если а - b + с = 0, или b = а + с, то х1 = - 1.
Пример.345х2 - 137х - 208 = 0. Так как а + b + с = 0 (345 - 137 - 208 = 0), то х1 = 1, х2 = -208/345.
Ответ: х1=1; х2 = -208/345 . Пример.132х2 + 247х + 115 = 0 Т.к. a-b+с = 0 (132 - 247 +115=0), то х1= - 1, х2= - 115/132 Ответ: х1= - 1; х2=- 115/132.
Существуют и другие свойства коэффициентов квадратного уравнения. но их использование более сложное.
Рассмотрим геометрический способ решения квадратных уравнений.
Пример.
х2 + 10х = 39. В оригинале эта задача формулируется следующим образом: "Квадрат и десять корней равны 39".
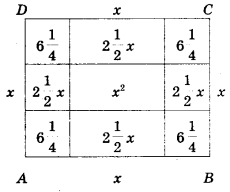
Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5,
следовательно, площадь каждого равна 2,5x. Полученную фигуру дополняют затем до нового квадрата АВСD,
достраивая в углах четыре равных квадрата, сторона каждого из них 2,5, а площадь 6,25.
Рисунок:
Графический способ решения уравнения х2 + 10х = 39
Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х2, четырех прямоугольников (4∙2,5x = 10х) и
четырех пристроенных квадратов (6,25∙ 4 = 25) , т.е. S = х2 + 10х = 25. Заменяя х2 + 10х числом 39, получим что S = 39+ 25 = 64,
откуда следует, что сторона квадрата АВСD, т.е. отрезок АВ = 8.
Для искомой стороны х первоначального квадрата получим x=8-2,5-2,5=3.
Рассмотрим решение квадратных уравнений при помощи теоремы Безу.
Остаток от деления многочлена P(x) на двучлен x - α равен P(α) (т.е. значению P(x) при x = α). Если число α является корнем многочлена P(x),
то этот многочлен делится на x -α без остатка. Пример.х²-4х+3=0 Р(x)= х²-4х+3, α: ±1,±3, α =1, 1-4+3=0.
Разделим Р(x) на (х-1):(х²-4х+3)/(х-1)=х-3 х²-4х+3=(х-1)(х-3), (х-1)(х-3)=0 х-1=0; х=1, или х-3=0, х=3; Ответ: х1=2, х2=3.
Вывод: Умение быстро и рационально решать квадратные уравнения просто необходимо для решения более сложных уравнений,
например, дробно-рациональных уравнений, уравнений высших степеней, биквадратных уравнений, а в старшей школе тригонометрических,
показательных и логарифмических уравнений. Изучив все найденные способы решения квадратных уравнений,
мы можем посоветовать одноклассникам, кроме стандартных способов, решение способом переброски (6) и решение
уравнений по свойству коэффициентов (7), так как они являются более доступными для понимания.