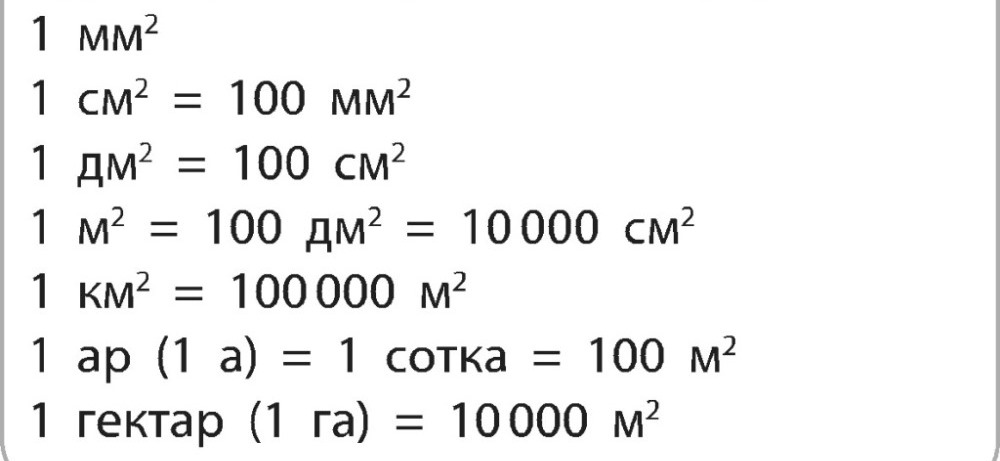Результаты исследования учащихся в проекте "Площадь прямоугольника": различия между версиями
(→Цели исследования) |
|||
| Строка 55: | Строка 55: | ||
[[Файл:Площадь5.jpg]] | [[Файл:Площадь5.jpg]] | ||
| + | |||
| + | '''3. Практическое применение формулы''' | ||
| + | |||
| + | Площадь прямоугольника: | ||
| + | |||
| + | S = a • b | ||
| + | |||
| + | a = S : b | ||
| + | |||
| + | Площадь квадрата: | ||
| + | |||
| + | S = a • a | ||
| + | |||
| + | |||
| + | |||
| + | Пример 1. Периметр прямоугольника равен 16 см. Длина прямоугольника равна 5 см. Чему равна площадь прямоугольника? | ||
| + | |||
| + | Краткое условие: | ||
| + | |||
| + | Р = 16 см | ||
| + | |||
| + | а = 5 см | ||
| + | |||
| + | S - ? | ||
| + | |||
| + | Рисунок к задаче: | ||
| + | |||
| + | b = S : a | ||
| + | |||
| + | [[Файл:Площадь6.jpg]] | ||
| + | |||
| + | Решение: | ||
| + | |||
| + | 1 способ | ||
| + | |||
| + | 1)16 : 2 = 8 (см) – половина Р | ||
| + | |||
| + | 2)8 – 5 = 3 (см) – ширина | ||
| + | |||
| + | 3)5 • 3 = 15 (см2) - S | ||
| + | |||
| + | 2 способ | ||
| + | |||
| + | 1)5 • 2 = 10 (см) – удвоенная длина | ||
| + | |||
| + | 2)16 – 10 = 6 (см) – удвоенная ширина | ||
| + | |||
| + | 3)6 : 2 = 3 (см) – ширина | ||
| + | |||
| + | 4)5 • 3 = 15 (см2) – S | ||
| + | |||
| + | Ответ: 15 см2. | ||
| + | |||
| + | |||
| + | |||
| + | Пример 2. Площадь прямоугольника равна 32 см2, а его длина – 8 см. Найти периметр прямоугольника. | ||
| + | |||
| + | Краткое условие: | ||
| + | |||
| + | S = 32 см2 | ||
| + | |||
| + | а = 8 см | ||
| + | |||
| + | Р - ? | ||
| + | |||
| + | Рисунок к задаче: | ||
==Вывод== | ==Вывод== | ||
Версия 16:16, 17 октября 2016
Содержание
Авторы и участники проекта
Шапошникова Марина Никулина Ирина
Участники группы "Историки"
Тема исследования группы
История возникновения формулы площади прямолугольника
Проблемный вопрос (вопрос для исследования)
Когда и как ученые пришли к современной интерпретации формулы площади прямоугольника?
Цели исследования
1.Ответить на вопросы: Историческая справка? Что такое площадь? Какими свойствами обладают площади фигур? Какие единицы измерения площади используются?
2.Научиться находить площадь прямоугольника и квадрата
3.Научиться пользоваться свойствами площадей при решении практических задач
Результаты проведённого исследования
1.Исторический очерк Многие годы площадь считалась первичным понятием, не требующим определения. Основной задачей математиков являлось вычисление площади, при этом были известны основные свойства площади. В Древнем Египте использовались точные правила вычисления площади прямоугольников, прямоугольных треугольников и трапеций, площадь произвольного четырёхугольника определялась приближённо как произведение полусумм пар противоположных сторон. Применение такой приближённой формулы связано с тем, что участки, площадь которых надо было померить, были в основном близки к прямоугольным и погрешность в таком случае оставалась небольшой. Историк математики А. П. Юшкевич предполагает, что египтяне могли и не знать, что пользуются приближённой формулой. В задаче 50 папируса Ринда содержится формула вычисления площади круга, которая считалась равной площади квадрата со стороной 8/9 диаметра круга. Такими же формулами пользовались и в Вавилоне, однако для площади круга приближение было менее точным. Кроме того, вавилоняне могли приближённо посчитать площади правильных пяти-, шести- и семиугольника со стороной равной единице. В шестидесятиричной системе им соответствовали 1,40, 2,37,20 и 3,41, соответственно.
Основным приёмом вычисления площади при этом являлось построение квадрата, площадь которого равна площади заданной многоугольной фигуры. Исторически вычисление площади называлось квадратурой.
2.Что такое площадь? Площадь фигуры - величина,показывающая сколько места занимает фигура на плоскости. Площадь измеряется квадратными величинами.
Свойство площади: 1.За единицу площади принимают площадь квадрата со стороной, равной единичному отрезку.1 см2 – квадрат со стороной 1 см.
2.Равные фигуры имеют равные площади.
Фигуры могут иметь равные площади, но не быть равны. Такие фигуры называются равновеликими.
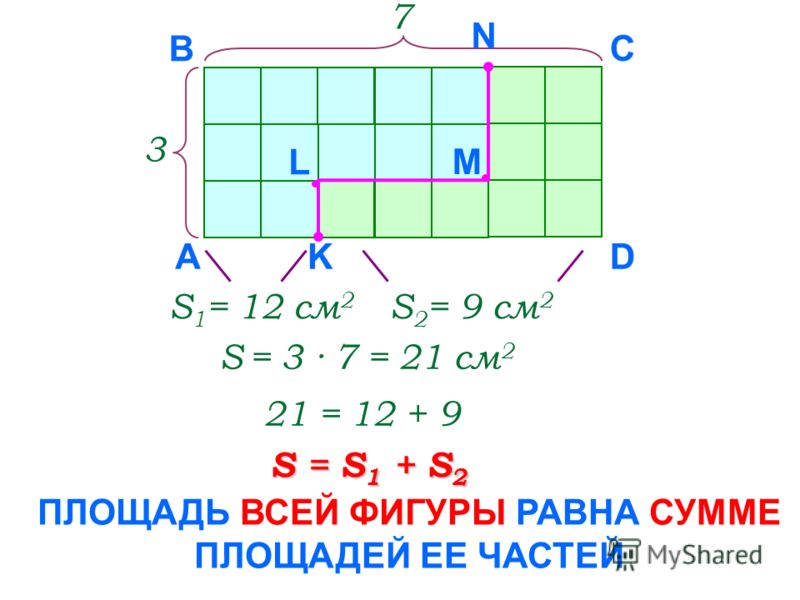
3.Площадь всей фигуры равна сумме площадей еѐ частей.
4. Единицы измерения площади
3. Практическое применение формулы
Площадь прямоугольника:
S = a • b
a = S : b
Площадь квадрата:
S = a • a
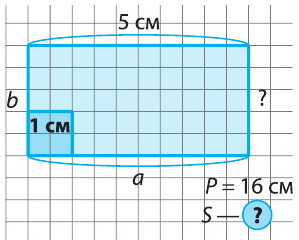
Пример 1. Периметр прямоугольника равен 16 см. Длина прямоугольника равна 5 см. Чему равна площадь прямоугольника?
Краткое условие:
Р = 16 см
а = 5 см
S - ?
Рисунок к задаче:
b = S : a
Решение:
1 способ
1)16 : 2 = 8 (см) – половина Р
2)8 – 5 = 3 (см) – ширина
3)5 • 3 = 15 (см2) - S
2 способ
1)5 • 2 = 10 (см) – удвоенная длина
2)16 – 10 = 6 (см) – удвоенная ширина
3)6 : 2 = 3 (см) – ширина
4)5 • 3 = 15 (см2) – S
Ответ: 15 см2.
Пример 2. Площадь прямоугольника равна 32 см2, а его длина – 8 см. Найти периметр прямоугольника.
Краткое условие:
S = 32 см2
а = 8 см
Р - ?
Рисунок к задаче: