Результаты исследований учащихся в проекте Учимся программировать: различия между версиями
(→Другие документы) |
(→Результаты проведённого исследования) |
||
| Строка 47: | Строка 47: | ||
[http://www.classtools.net/widgets/fishbone_2/wEg12.htm Ментальная карта "Рыбий скелет"]<br> | [http://www.classtools.net/widgets/fishbone_2/wEg12.htm Ментальная карта "Рыбий скелет"]<br> | ||
[[Изображение:Рыбий_скелет_Сколов_Васильев.jpg|600px]] | [[Изображение:Рыбий_скелет_Сколов_Васильев.jpg|600px]] | ||
| + | |||
| + | |||
| + | == Постановка задачи == | ||
| + | Целью нашего проекта является проверка второго закона Кеплера: "Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади." | ||
| + | Применительное к нашей Солнечной системе, с этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий — наиболее удалённая точка орбиты. Таким образом, из второго закона Кеплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии большую линейную скорость, чем в афелии.<br> | ||
| + | [[Изображение:СоколовВасильевВторойЗаконКеплера.svg.png]] | ||
| + | Наша экспериментальная модель будет представлять собой спутник, вращающийся вокруг Земли. | ||
| + | |||
| + | |||
| + | == Аналитическое решение == | ||
| + | |||
| + | |||
| + | По определению угловой момент \mathbf{L} точечной частицы с массой m и скоростью \mathbf{v} записывается в виде: | ||
| + | |||
| + | \mathbf{L} \ \stackrel{\mathrm{def}}{=}\ \mathbf{r} \times \mathbf{p} = \mathbf{r} \times ( m \mathbf{v} ). | ||
| + | |||
| + | где \mathbf{r} — радиус-вектор частицы а \mathbf{p} = m \mathbf{v} — импульс частицы. Площадь, заметаемая радиус-вектором \mathbf{r} за время dt из геометрических соображений равна dS=\frac{1}{2}r\sin\theta v dt=\frac{1}{2}|\mathbf{r}\times\mathbf{v}| dt=\frac{\mathbf{|L|}}{2m}dt, где \theta представляет собой угол между направлениями \mathbf{r} и \mathbf{v}. | ||
| + | |||
| + | По определению | ||
| + | |||
| + | \mathbf{v} = \frac{d\mathbf{r}}{dt} . | ||
| + | |||
| + | В результате мы имеем | ||
| + | |||
| + | \mathbf{L} = \mathbf{r} \times m\frac{d\mathbf{r}}{dt}. | ||
| + | |||
| + | Продифференцируем обе части уравнения по времени | ||
| + | |||
| + | \frac{d\mathbf{L}}{dt} = (\mathbf{r} \times \mathbf{F}) + \left( \frac{d\mathbf{r}}{dt} \times m\frac{d\mathbf{r}}{dt} \right) = ( \mathbf{r} \times \mathbf{F} ) + ( \mathbf{v} \times \mathbf{p} ) = 0 | ||
| + | |||
| + | поскольку векторное произведение параллельных векторов равно нулю. Заметим, что F всегда параллелен r, поскольку сила радиальная, и p всегда параллелен v по определению. Таким образом можно утверждать, что |\mathbf{L}|, а следовательно и пропорциональная ей скорость заметания площади \frac{dS}{dt} — константа. | ||
==Вывод== | ==Вывод== | ||
Версия 15:57, 18 декабря 2013
Содержание
Авторы и участники проекта
Тема исследования группы
Моделирование физических явлений с помощью программ в рамках проекта "Учимся программировать"
Проблемный вопрос (вопрос для исследования)
Как в вашей области используется программы?
Гипотеза исследования
Мы считаем что, профессия "программист" весьма востребована в современном информационном обществе. Программисты пользуются спросом во всех научных и социальных областях, в том числе и физике. Все научно-исследовательские институты пользуются услугами программистов для точного вычисления физических констант путем моделирования естественных процессов.К примеру на супер компьютерах была поставлена гипотеза существования "Базона Хикса", которая, в последствии, была успешно проверенна на большом адронном коллайдере.
Цели исследования
- В соответствии с проблемным вопросом выбрать физические явления, моделирование которых будет производится на программах, написанных на языке С++.
- Аналитически интерпретировать поставленную задачу.
- Выделить ключевые пункты моделируемого явления.
- Проанализировать полученные результаты и составить рабочую программу исследуемого явления.
Результаты проведённого исследования
5-6 абзацев текста по целям
Ментальная карта "Рыбий скелет"
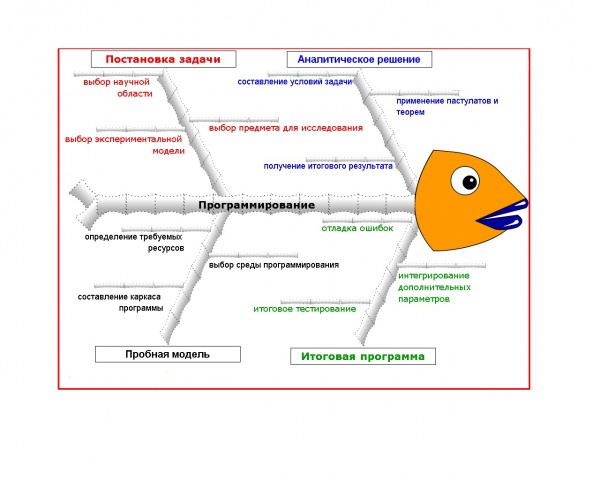
Постановка задачи
Целью нашего проекта является проверка второго закона Кеплера: "Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади."
Применительное к нашей Солнечной системе, с этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий — наиболее удалённая точка орбиты. Таким образом, из второго закона Кеплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии большую линейную скорость, чем в афелии.
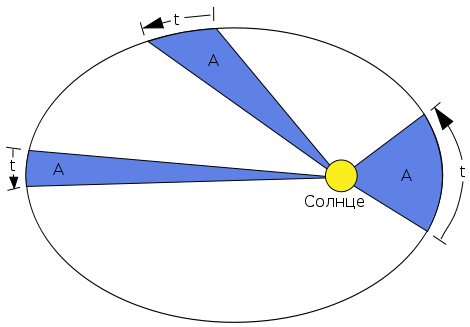Наша экспериментальная модель будет представлять собой спутник, вращающийся вокруг Земли.
Аналитическое решение
По определению угловой момент \mathbf{L} точечной частицы с массой m и скоростью \mathbf{v} записывается в виде:
\mathbf{L} \ \stackrel{\mathrm{def}}{=}\ \mathbf{r} \times \mathbf{p} = \mathbf{r} \times ( m \mathbf{v} ).
где \mathbf{r} — радиус-вектор частицы а \mathbf{p} = m \mathbf{v} — импульс частицы. Площадь, заметаемая радиус-вектором \mathbf{r} за время dt из геометрических соображений равна dS=\frac{1}{2}r\sin\theta v dt=\frac{1}{2}|\mathbf{r}\times\mathbf{v}| dt=\frac{\mathbf{|L|}}{2m}dt, где \theta представляет собой угол между направлениями \mathbf{r} и \mathbf{v}.
По определению
\mathbf{v} = \frac{d\mathbf{r}}{dt} .
В результате мы имеем
\mathbf{L} = \mathbf{r} \times m\frac{d\mathbf{r}}{dt}.
Продифференцируем обе части уравнения по времени
\frac{d\mathbf{L}}{dt} = (\mathbf{r} \times \mathbf{F}) + \left( \frac{d\mathbf{r}}{dt} \times m\frac{d\mathbf{r}}{dt} \right) = ( \mathbf{r} \times \mathbf{F} ) + ( \mathbf{v} \times \mathbf{p} ) = 0
поскольку векторное произведение параллельных векторов равно нулю. Заметим, что F всегда параллелен r, поскольку сила радиальная, и p всегда параллелен v по определению. Таким образом можно утверждать, что |\mathbf{L}|, а следовательно и пропорциональная ей скорость заметания площади \frac{dS}{dt} — константа.
Вывод
анализ результатов
Полезные ресурсы
Портал с большим количеством книг, справочников, примеров исходного кода, на языке С++
Основы программирования (алгоритмы, циклы, функции)
Ресурс состоит из видеороликов и практических занятий по С++, совмещенных с консультациями автора
Основы объектно-ориентированного программирования на С++
Учебник по вики
Сборник руководств по продуктам Microsoft Office
