Результаты исследования учащихся в проекте Осваиваем Delphi: различия между версиями
(→Постановка задачи "Интерполяция фунции") |
(→Полезные ресурсы) |
||
| (не показано 20 промежуточных версий 2 участников) | |||
| Строка 10: | Строка 10: | ||
== Гипотеза исследования == | == Гипотеза исследования == | ||
| − | + | Чтобы составить математическую модель необходимо выполнить формализацию задачи(представить её в виде математических соотношений) | |
==Цели исследования== | ==Цели исследования== | ||
| − | -Подобрать примеры задач из курса математики | + | -Подобрать примеры задач из курса математики для создания моделей на Delphi |
| − | -Выполнить постановку задачи | + | -Выполнить постановку задачи |
| − | -Разработать алгоритм | + | -Разработать алгоритм решения задачи |
| − | - | + | -Создать программу на Delphi |
| − | - | + | -Проанализировать полученные результаты |
==Результаты проведённого исследования== | ==Результаты проведённого исследования== | ||
Рассмотрим использование языка Delphi для решения математических задач на примере задачи | Рассмотрим использование языка Delphi для решения математических задач на примере задачи | ||
| − | + | интерполирования функции. | |
| − | + | '''Постановка задачи "Интерполяция фунции"''' | |
Задача интерполирования состоит в том, чтобы по значениям функции f(x) в некоторых точках отрезка восстановить ее значения в остальных точках отрезка. | Задача интерполирования состоит в том, чтобы по значениям функции f(x) в некоторых точках отрезка восстановить ее значения в остальных точках отрезка. | ||
Интерполирование применяется при сгущении таблиц, когда вычисление функции f(x) трудоемко и необходимо составить таблицу с меньшим шагом. | Интерполирование применяется при сгущении таблиц, когда вычисление функции f(x) трудоемко и необходимо составить таблицу с меньшим шагом. | ||
| − | Под интерполированием понимается нахождение аналитической кривой, проходящей через строго | + | |
| + | Под интерполированием понимается нахождение аналитической кривой, проходящей через строго заданное множество точек на плоскости. | ||
| + | |||
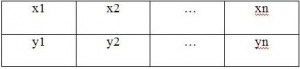
Пусть функция у=f(x)задана таблично. | Пусть функция у=f(x)задана таблично. | ||
| − | При этом требуется получить значение функции у=f(x) для такого значения аргумента х, которое входит в отрезок [х0, xn], но не совпадает ни с одним из значений | + | |
| − | Будем искать значение функции в точке z | + | [[Изображение:Таблица2.JPG|300px]] |
| + | |||
| + | При этом требуется получить значение функции у=f(x) для такого значения аргумента х, которое входит в отрезок [х0, xn], но не совпадает ни с одним из значений х<sub>i</sub> i=0, 1,2,.. ,n т.е. х [х0, хn], х≠х<sub>i</sub> , i=0, 1, 2,...,n. | ||
| + | Будем искать значение функции в точке х<sub>i</sub> < z < х<sub>i</sub>+1. | ||
| + | |||
Задача заключается в нахождении такого интерполирующего многочлена, значения которого в узлах интерполяции совпадут с соответствующими значениями функции. | Задача заключается в нахождении такого интерполирующего многочлена, значения которого в узлах интерполяции совпадут с соответствующими значениями функции. | ||
Одно из возможных методов – использование многочлена Лагранжа. | Одно из возможных методов – использование многочлена Лагранжа. | ||
| − | Функция | + | Функция φ<sub>j</sub> (z) носят название Лагранжовых коэффициентов. |
В данном программном комплексе задача интерполирования решается с помощью формулы | В данном программном комплексе задача интерполирования решается с помощью формулы | ||
| − | + | [[Изображение:Формула.JPG|300px]] | |
| + | |||
| + | '''Алгоритм решения задачи''' | ||
| + | |||
| + | алгоритм Интерполяция | ||
| + | |||
| + | Program Lagrange; | ||
| + | |||
| + | var i,j,n:integer; | ||
| + | |||
| + | lag,xp,z,p:real; | ||
| + | |||
| + | x,y:array [1..20] of real | ||
| + | |||
| + | begin | ||
| + | |||
| + | write('введите число узлов'); | ||
| + | |||
| + | readln(n); | ||
| + | |||
| + | write('введите точку, в которой ищем значение функции '); | ||
| + | |||
| + | readln(xp); | ||
| − | + | for i:=1 to n do | |
| − | + | begin | |
| − | + | write ('введите значение',i,'узла и значение функции в нем'); | |
| − | + | readln(x[i], y[i]); | |
| − | + | end; | |
| − | + | lag:=0; | |
| − | + | for i:=1 to n do | |
| − | + | begin | |
| − | + | p:=1; z:=1; | |
| − | + | for j:=1 to n do | |
| − | |||
| − | |||
| − | + | if i<>j then | |
| − | + | begin | |
| − | + | p:=p*(xp-x[j]); | |
| − | + | z:=z*(x[i]-x[j]); | |
| − | + | end; | |
| − | |||
| − | |||
| − | + | lag:=lag+y[i]*p/z; | |
| − | + | end; | |
| − | |||
| − | |||
| − | + | writeln('искомое значение в точке', xp:3,'равно',lag:5:1); | |
| − | + | end. | |
| − | |||
| − | |||
| − | + | '''Рассмотрим решение задачи на примере со стаканом с водой:''' | |
| − | + | В стакан с водой опустили нагреватель и сняли показания температуры воды в зависимости от времени. Полученные результаты занесли в таблицу: | |
| + | |||
| + | [[Изображение:Сухонина Результаты исследования.JPG]] | ||
| + | |||
| + | Нужно определить какая температура в стакане на 4-й минуте? | ||
| + | |||
| + | |||
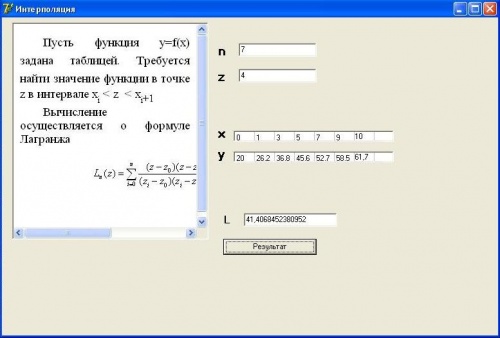
| + | '''Решение задачи на Delphi''' | ||
| + | |||
| + | |||
| + | [[Изображение:Форма Сухониной пример.JPG|500px]] | ||
==Вывод== | ==Вывод== | ||
| + | Использование языка Delphi является оправданным в решении математической модели, потому что модель представляется наглядно. | ||
| + | |||
| − | |||
== Другие документы == | == Другие документы == | ||
Текущая версия на 11:23, 12 декабря 2009
Содержание
Авторы и участники проекта
Сухонина Евгения, Бачинина Наталья и участники группы "Математики"
Тема исследования группы
Создаем математическую модель
Проблемный вопрос (вопрос для исследования)
Как на языке Delphi составить математическую модель?
Гипотеза исследования
Чтобы составить математическую модель необходимо выполнить формализацию задачи(представить её в виде математических соотношений)
Цели исследования
-Подобрать примеры задач из курса математики для создания моделей на Delphi
-Выполнить постановку задачи
-Разработать алгоритм решения задачи
-Создать программу на Delphi
-Проанализировать полученные результаты
Результаты проведённого исследования
Рассмотрим использование языка Delphi для решения математических задач на примере задачи интерполирования функции.
Постановка задачи "Интерполяция фунции"
Задача интерполирования состоит в том, чтобы по значениям функции f(x) в некоторых точках отрезка восстановить ее значения в остальных точках отрезка. Интерполирование применяется при сгущении таблиц, когда вычисление функции f(x) трудоемко и необходимо составить таблицу с меньшим шагом.
Под интерполированием понимается нахождение аналитической кривой, проходящей через строго заданное множество точек на плоскости.
Пусть функция у=f(x)задана таблично.
При этом требуется получить значение функции у=f(x) для такого значения аргумента х, которое входит в отрезок [х0, xn], но не совпадает ни с одним из значений хi i=0, 1,2,.. ,n т.е. х [х0, хn], х≠хi , i=0, 1, 2,...,n. Будем искать значение функции в точке хi < z < хi+1.
Задача заключается в нахождении такого интерполирующего многочлена, значения которого в узлах интерполяции совпадут с соответствующими значениями функции. Одно из возможных методов – использование многочлена Лагранжа. Функция φj (z) носят название Лагранжовых коэффициентов. В данном программном комплексе задача интерполирования решается с помощью формулы
Алгоритм решения задачи
алгоритм Интерполяция
Program Lagrange;
var i,j,n:integer;
lag,xp,z,p:real;
x,y:array [1..20] of real
begin
write('введите число узлов');
readln(n);
write('введите точку, в которой ищем значение функции ');
readln(xp);
for i:=1 to n do
begin
write ('введите значение',i,'узла и значение функции в нем');
readln(x[i], y[i]);
end;
lag:=0;
for i:=1 to n do
begin
p:=1; z:=1;
for j:=1 to n do
if i<>j then
begin
p:=p*(xp-x[j]);
z:=z*(x[i]-x[j]);
end;
lag:=lag+y[i]*p/z;
end;
writeln('искомое значение в точке', xp:3,'равно',lag:5:1);
end.
Рассмотрим решение задачи на примере со стаканом с водой:
В стакан с водой опустили нагреватель и сняли показания температуры воды в зависимости от времени. Полученные результаты занесли в таблицу:
Нужно определить какая температура в стакане на 4-й минуте?
Решение задачи на Delphi
Вывод
Использование языка Delphi является оправданным в решении математической модели, потому что модель представляется наглядно.