Результаты исследования обучающихся в проекте "Делимость натуральных чисел": различия между версиями
(→Результаты проведённого исследования) |
(→Результаты проведённого исследования) |
||
| (не показано 6 промежуточных версий этого же участника) | |||
| Строка 8: | Строка 8: | ||
==Тема исследования группы== | ==Тема исследования группы== | ||
| + | Делимость натуральных чисел | ||
== Проблемный вопрос (вопрос для исследования)== | == Проблемный вопрос (вопрос для исследования)== | ||
| Строка 14: | Строка 15: | ||
== Гипотеза исследования == | == Гипотеза исследования == | ||
| − | мы считаем, что | + | мы считаем, что признаки делимости появились вместе с появлением и развитием самих чисел |
==Цели исследования== | ==Цели исследования== | ||
1.Познакомиться с историей возникновения признаков делимости натуральных чисел. | 1.Познакомиться с историей возникновения признаков делимости натуральных чисел. | ||
| − | 2. Узнать | + | 2. Узнать об ученых, занимавшихся изучением делимости чисел |
3. Построить ленту времени "Возникновение признаков делимости" | 3. Построить ленту времени "Возникновение признаков делимости" | ||
| Строка 42: | Строка 43: | ||
Признаки делимости на 2, 3 и 5 были известны с давних времен. Так, например, признак делимости на 2 знали древние египтяне за две тысячи лет до нашей эры, а признак делимости на 9 был известен грекам в третьем столетии до нашей эры. Впервые признаки делимости на 2, 3 и 5 были обстоятельно изложены итальянским математиком Леонардо Фибоначчи (около 1179 – 1228). Выдающийся французский математик и физик Блез Паскаль (1623 – 1662) еще в раннем возрасте вывел общий признак делимости чисел, из которого следуют все частные признаки. | Признаки делимости на 2, 3 и 5 были известны с давних времен. Так, например, признак делимости на 2 знали древние египтяне за две тысячи лет до нашей эры, а признак делимости на 9 был известен грекам в третьем столетии до нашей эры. Впервые признаки делимости на 2, 3 и 5 были обстоятельно изложены итальянским математиком Леонардо Фибоначчи (около 1179 – 1228). Выдающийся французский математик и физик Блез Паскаль (1623 – 1662) еще в раннем возрасте вывел общий признак делимости чисел, из которого следуют все частные признаки. | ||
| − | Признаки делимости на 2, 3 и 5 были обстоятельно изложены итальянским математиком | + | Признаки делимости на 2, 3 и 5 были обстоятельно изложены итальянским математиком [https://ru.wikipedia.org/wiki/ФибоначчиЛеонардо Фибоначчи (1170 – 1228)].[[изображение:Леонардо МОВ.jpg|150px]] |
В III веке до нашей эры александрийский ученый [https://ru.wikipedia.org/wiki/Эратосфен Эратосфен] открыл способ составления списка простых чисел, так как считал, что простые числа играют важную роль в изучении всех остальных чисел. Его метод составления списка простых чисел назвали решетом Эратосфена. | В III веке до нашей эры александрийский ученый [https://ru.wikipedia.org/wiki/Эратосфен Эратосфен] открыл способ составления списка простых чисел, так как считал, что простые числа играют важную роль в изучении всех остальных чисел. Его метод составления списка простых чисел назвали решетом Эратосфена. | ||
| Строка 51: | Строка 52: | ||
Паскаль нашел общий алгоритм для нахождения признаков делимости любого целого числа на любое другое целое число, который опубликовал в трактате "О характере делимости чисел". | Паскаль нашел общий алгоритм для нахождения признаков делимости любого целого числа на любое другое целое число, который опубликовал в трактате "О характере делимости чисел". | ||
| + | |||
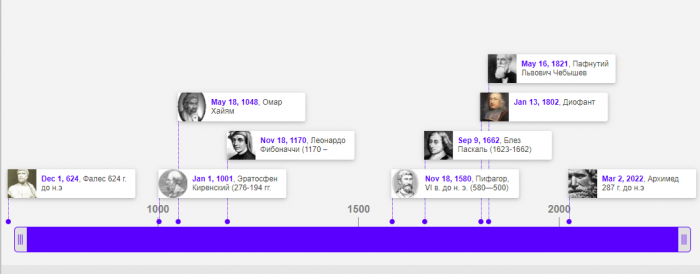
| + | [https://www.timetoast.com/timelines/--1176 Лента времени "История делимости чисел"] | ||
| + | |||
| + | [[Файл:2022-03-11 10-27-07.png | 700px ]] | ||
==Вывод== | ==Вывод== | ||
| + | Значимость признаков делимости в математике бесспорна. Ведь именно с помощью признаков делимости можно узнать, делится ли одно число на другое без остатка, не производя фактического деления. Также знание признаков делимости позволяет быстро находить НОК (Наименьшее Общее Кратное) и НОД (Наибольший Общий Делитель), а это не менее важно. | ||
| + | Делимость натуральных чисел, простые и составные числа, взаимно простые числа, делители и кратные, разложение чисел на простые множители интересовали великих математиков еще с древних времен. Признаки делимости на 2, 3, 5, 9, 10, были известны с давних времен. Признак делимости на 2 знали древние египтяне за 2 тысячи лет до нашей эры. | ||
==Полезные ресурсы== | ==Полезные ресурсы== | ||
Текущая версия на 10:34, 11 марта 2022
Содержание
Авторы и участники проекта
участники группы историки
Тема исследования группы
Делимость натуральных чисел
Проблемный вопрос (вопрос для исследования)
Какова история возникновения делимости натуральных чисел?
Гипотеза исследования
мы считаем, что признаки делимости появились вместе с появлением и развитием самих чисел
Цели исследования
1.Познакомиться с историей возникновения признаков делимости натуральных чисел.
2. Узнать об ученых, занимавшихся изучением делимости чисел
3. Построить ленту времени "Возникновение признаков делимости"
Результаты проведённого исследования
С древних времен человечество интересовалось числами. Люди научились считать еще в каменном веке. Конечно, это были весьма примитивные приемы счета – на пальцах, с помощью зарубок и так далее.
С развитием цивилизации познания людей в математике расширялись. Развивалась торговля, людям нужно было уметь считать товар и деньги, чтобы не быть обманутыми.
Постепенно стали возникать математические принципы, например такие:
- Два любых натуральных числа всегда можно сложить, а также умножить.
- Из одного натурального числа можно вычесть другое, но лишь тогда, когда вычитаемое меньше уменьшаемого.
- С делением несколько сложнее. Деление без остатка можно выполнить только для некоторых чисел, причем бывает довольно трудно заранее узнать, делится ли одно число на другое. Помимо того, есть числа, которые делятся только на единицу или сами на себя. Они называются «простыми» числами. А делить на ноль и вовсе нельзя.
В современной жизни у нас часто возникает необходимость узнать, делится ли одно число на другое без остатка. Не всегда под рукой имеются технические средства, чтобы это быстро рассчитать. Для подсчета без калькулятора можно использовать признаки делимости.
Признак делимости — правило, позволяющее сравнительно быстро определить, является ли число кратным заранее заданному числу без необходимости выполнять фактическое деление.
Признаки делимости на 2, 3 и 5 были известны с давних времен. Так, например, признак делимости на 2 знали древние египтяне за две тысячи лет до нашей эры, а признак делимости на 9 был известен грекам в третьем столетии до нашей эры. Впервые признаки делимости на 2, 3 и 5 были обстоятельно изложены итальянским математиком Леонардо Фибоначчи (около 1179 – 1228). Выдающийся французский математик и физик Блез Паскаль (1623 – 1662) еще в раннем возрасте вывел общий признак делимости чисел, из которого следуют все частные признаки.
Признаки делимости на 2, 3 и 5 были обстоятельно изложены итальянским математиком Фибоначчи (1170 – 1228).
В III веке до нашей эры александрийский ученый Эратосфен открыл способ составления списка простых чисел, так как считал, что простые числа играют важную роль в изучении всех остальных чисел. Его метод составления списка простых чисел назвали решетом Эратосфена.
Вопросы делимости чисел рассматривались учениками Пифагора.
 Большой вклад в изучение признаков делимости чисел внес Блез Паскаль, один из самых знаменитых людей в истории человечества. Паскаль родился 19 июня 1623 в Клермон-Ферран, в семье высокообразованного юриста. Отец Паскаля имел хорошее образование и решил самостоятельно заниматься образованием мальчика. Блез рос одарённым ребёнком и рано проявил выдающиеся математические способности. Его отец старался обучить мальчика древним языкам, настаивая, чтобы тот не отвлекался на разного рода пустяки. Как-то раз, на очередной вопрос сына о том, что такое геометрия, отец кратко ответил, что это способ чертить правильные фигуры и находить между ними пропорции. Однако тут же запретил ему всякие исследования в этой области. Но запретный плод сладок, и Блез, закрывшись в своей спальне, принялся углем выводить на полу различные фигуры и изучать их. Когда отец случайно застал его за одним из таких самостоятельных уроков, он был потрясен: не знавший даже названий фигур, мальчик доказывал их свойства. Так постепенно раскрывался гений Блеза Паскаля.
Большой вклад в изучение признаков делимости чисел внес Блез Паскаль, один из самых знаменитых людей в истории человечества. Паскаль родился 19 июня 1623 в Клермон-Ферран, в семье высокообразованного юриста. Отец Паскаля имел хорошее образование и решил самостоятельно заниматься образованием мальчика. Блез рос одарённым ребёнком и рано проявил выдающиеся математические способности. Его отец старался обучить мальчика древним языкам, настаивая, чтобы тот не отвлекался на разного рода пустяки. Как-то раз, на очередной вопрос сына о том, что такое геометрия, отец кратко ответил, что это способ чертить правильные фигуры и находить между ними пропорции. Однако тут же запретил ему всякие исследования в этой области. Но запретный плод сладок, и Блез, закрывшись в своей спальне, принялся углем выводить на полу различные фигуры и изучать их. Когда отец случайно застал его за одним из таких самостоятельных уроков, он был потрясен: не знавший даже названий фигур, мальчик доказывал их свойства. Так постепенно раскрывался гений Блеза Паскаля.
Паскаль нашел общий алгоритм для нахождения признаков делимости любого целого числа на любое другое целое число, который опубликовал в трактате "О характере делимости чисел".
Лента времени "История делимости чисел"
Вывод
Значимость признаков делимости в математике бесспорна. Ведь именно с помощью признаков делимости можно узнать, делится ли одно число на другое без остатка, не производя фактического деления. Также знание признаков делимости позволяет быстро находить НОК (Наименьшее Общее Кратное) и НОД (Наибольший Общий Делитель), а это не менее важно. Делимость натуральных чисел, простые и составные числа, взаимно простые числа, делители и кратные, разложение чисел на простые множители интересовали великих математиков еще с древних времен. Признаки делимости на 2, 3, 5, 9, 10, были известны с давних времен. Признак делимости на 2 знали древние египтяне за 2 тысячи лет до нашей эры.
Полезные ресурсы
3 признаки делимости натуральных чисел