Результаты исследования обучающихся в проекте Комбинаторика: различия между версиями
(→Результаты проведённого исследования) |
(→Полезные ресурсы) |
||
| (не показаны 4 промежуточные версии 2 участников) | |||
| Строка 29: | Строка 29: | ||
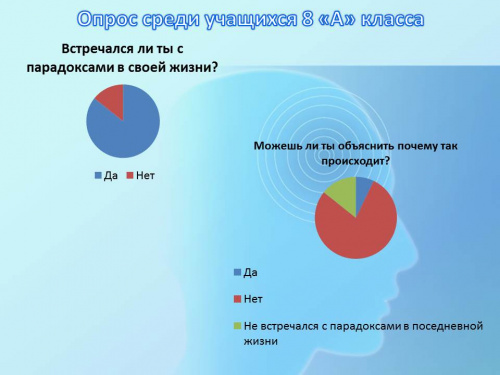
1. Учащиеся видят непосредственную связь математики с окружающей действительностью, реальной жизнью, но не умеют применять это на практике. Поэтому мы решили провести опрос, чтобы выявить уровень их ориентированности в данной теме. В ходе опроса было видно, что ребятам интересна данная тема. В результате было выявлено, что учащиеся часто встречаются с парадоксами теории вероятности, но не знают, как это происходит. Следовательно, не могут применить их в жизни. | 1. Учащиеся видят непосредственную связь математики с окружающей действительностью, реальной жизнью, но не умеют применять это на практике. Поэтому мы решили провести опрос, чтобы выявить уровень их ориентированности в данной теме. В ходе опроса было видно, что ребятам интересна данная тема. В результате было выявлено, что учащиеся часто встречаются с парадоксами теории вероятности, но не знают, как это происходит. Следовательно, не могут применить их в жизни. | ||
| + | |||
[[Изображение:Учебный проект по комбинаторике опрос 1.jpeg| 500px]] | [[Изображение:Учебный проект по комбинаторике опрос 1.jpeg| 500px]] | ||
[[Изображение:Учебный проект по комбинаторике опрос 2.jpeg| 500px]] | [[Изображение:Учебный проект по комбинаторике опрос 2.jpeg| 500px]] | ||
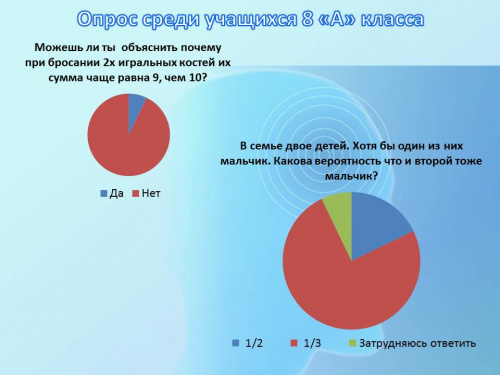
2. Выводы теории вероятностей находят применение в повседневной жизни, науке, технике и т.д. В повседневной жизни нам постоянно приходится сталкиваться со случайностью, и теория вероятностей учит нас, как действовать рационально с учетом риска, связанного с принятием отдельных решений. Современный образованный человек независимо от профессии и рода занятий должен быть знаком с простейшими понятиями теории вероятностей. В наши дни, когда прогноз погоды содержит сообщение о вероятности дождя на завтра, каждый должен знать что собственно это означает. Возьмем, к примеру, игру в монету. При бросании может быть два равновероятных исхода: монета может упасть кверху гербом или решкой. Бросая монету один раз нельзя предугадать, какая сторона окажется сверху. Однако, бросив монету 100 раз, можно сделать выводы. Можно заранее сказать, что герб выпадет не 1 и не 2 раза, а больше, но и не 99 и не 98 раз, а меньше. Число выпадений герба будет близко к 50. На самом деле, и на опыте можно в этом убедиться, что это число будет заключено между 40 и 60. | 2. Выводы теории вероятностей находят применение в повседневной жизни, науке, технике и т.д. В повседневной жизни нам постоянно приходится сталкиваться со случайностью, и теория вероятностей учит нас, как действовать рационально с учетом риска, связанного с принятием отдельных решений. Современный образованный человек независимо от профессии и рода занятий должен быть знаком с простейшими понятиями теории вероятностей. В наши дни, когда прогноз погоды содержит сообщение о вероятности дождя на завтра, каждый должен знать что собственно это означает. Возьмем, к примеру, игру в монету. При бросании может быть два равновероятных исхода: монета может упасть кверху гербом или решкой. Бросая монету один раз нельзя предугадать, какая сторона окажется сверху. Однако, бросив монету 100 раз, можно сделать выводы. Можно заранее сказать, что герб выпадет не 1 и не 2 раза, а больше, но и не 99 и не 98 раз, а меньше. Число выпадений герба будет близко к 50. На самом деле, и на опыте можно в этом убедиться, что это число будет заключено между 40 и 60. | ||
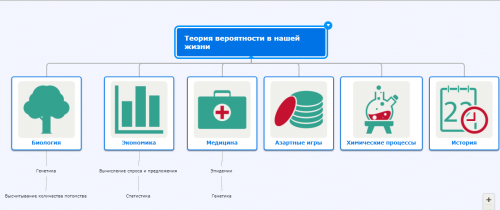
| + | [https://www.mindomo.com/ru/mindmap/2a75575904644d04bda6921e0843d66f Области применения теории вероятности] | ||
| + | |||
| + | [[Изображение:Области применения ТерВер.png| 500px]] | ||
3. В ходе работы были рассмотрены два типа парадоксов. В теории вероятностей парадоксы бывают двух типов: первый — когда существует строгое решение в рамках аксиоматики, просто оно не очевидно, и условия задачи таковы, что ведут интуитивное понимание условий в ошибочном ключе, примерами таких парадоксов являются — [https://docs.google.com/document/d/1zA6mpNSo3HWzezgoQ8caSROK7QXBWdXrh_TaKQAwKGs/edit?usp=sharing парадокс игры в кости], [https://docs.google.com/document/d/1-gITofjRmpx4tu5J9Up5YnuIt-F76mQtscQbRfaq8h0/edit?usp=sharing Санкт-Петербургский парадокс], [https://docs.google.com/document/d/1cQusrBOMniq5D1R7vDHxzYrExWJX4ct3Mt6RxpwyLGE/edit?usp=sharing Парадокс закона больших чисел Бернулли], [https://docs.google.com/document/d/1a8imoywKBGKJ0QgiPXaBG23uiTs4QIYcuAon9VVLhe4/edit?usp=sharing Парадокс раздачи подарков]; второй тип — парадоксы, которые основываются на неоднозначной интерпретации аксиоматики теории вероятности, её недоопределённости, которую отмечал еще Пуанкаре, их и можно назвать истинными парадоксами. Примеры истинных парадоксов: [https://docs.google.com/document/d/1mYgtg_n3rYeimmIoBVkdw9mPLo8fKXA5g_Q9takXO-4/edit?usp=sharing Проблема Монти Холла], [https://docs.google.com/document/d/1fVwxzRlXbr_AQuJbvCG8Y2MS_Qp2lN0MTjOYlQbfZGo/edit?usp=sharing Парадокс мальчика и девочки]. Ценность обоих типов парадоксов в том, что они помогают лучше понять суть теории, область её ограничения, глубже понять основания теории, и иногда исследование парадоксов вело к созданию отдельных разделов математики. | 3. В ходе работы были рассмотрены два типа парадоксов. В теории вероятностей парадоксы бывают двух типов: первый — когда существует строгое решение в рамках аксиоматики, просто оно не очевидно, и условия задачи таковы, что ведут интуитивное понимание условий в ошибочном ключе, примерами таких парадоксов являются — [https://docs.google.com/document/d/1zA6mpNSo3HWzezgoQ8caSROK7QXBWdXrh_TaKQAwKGs/edit?usp=sharing парадокс игры в кости], [https://docs.google.com/document/d/1-gITofjRmpx4tu5J9Up5YnuIt-F76mQtscQbRfaq8h0/edit?usp=sharing Санкт-Петербургский парадокс], [https://docs.google.com/document/d/1cQusrBOMniq5D1R7vDHxzYrExWJX4ct3Mt6RxpwyLGE/edit?usp=sharing Парадокс закона больших чисел Бернулли], [https://docs.google.com/document/d/1a8imoywKBGKJ0QgiPXaBG23uiTs4QIYcuAon9VVLhe4/edit?usp=sharing Парадокс раздачи подарков]; второй тип — парадоксы, которые основываются на неоднозначной интерпретации аксиоматики теории вероятности, её недоопределённости, которую отмечал еще Пуанкаре, их и можно назвать истинными парадоксами. Примеры истинных парадоксов: [https://docs.google.com/document/d/1mYgtg_n3rYeimmIoBVkdw9mPLo8fKXA5g_Q9takXO-4/edit?usp=sharing Проблема Монти Холла], [https://docs.google.com/document/d/1fVwxzRlXbr_AQuJbvCG8Y2MS_Qp2lN0MTjOYlQbfZGo/edit?usp=sharing Парадокс мальчика и девочки]. Ценность обоих типов парадоксов в том, что они помогают лучше понять суть теории, область её ограничения, глубже понять основания теории, и иногда исследование парадоксов вело к созданию отдельных разделов математики. | ||
| Строка 49: | Строка 53: | ||
#[https://support.office.com/ru-ru/article/%D0%94%D0%BE%D0%B1%D0%B0%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5-%D0%B4%D0%B8%D0%B0%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D1%8B-%D0%B2-%D0%B4%D0%BE%D0%BA%D1%83%D0%BC%D0%B5%D0%BD%D1%82-word-ff48e3eb-5e04-4368-a39e-20df7c798932 Создание диаграмм] | #[https://support.office.com/ru-ru/article/%D0%94%D0%BE%D0%B1%D0%B0%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5-%D0%B4%D0%B8%D0%B0%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D1%8B-%D0%B2-%D0%B4%D0%BE%D0%BA%D1%83%D0%BC%D0%B5%D0%BD%D1%82-word-ff48e3eb-5e04-4368-a39e-20df7c798932 Создание диаграмм] | ||
#[http://pedsovet.su/metodika/priemy/5673_metod_klaster_na_uroke Как создать диаграмму] | #[http://pedsovet.su/metodika/priemy/5673_metod_klaster_na_uroke Как создать диаграмму] | ||
| + | #[https://ru.wikipedia.org/wiki/%D0%92%D0%B8%D0%BA%D0%B8%D0%BF%D0%B5%D0%B4%D0%B8%D1%8F:%D0%A1%D0%BF%D0%B8%D1%81%D0%BE%D0%BA_%D0%BF%D1%80%D0%B0%D0%B2%D0%B8%D0%BB Правила работы в Вики] | ||
== Другие документы == | == Другие документы == | ||
Текущая версия на 09:04, 17 июня 2019
Содержание
Авторы и участники проекта
- Медведева Анна
- Волкова Аня
- Участники группы Теоретики
Тема исследования группы
Вероятностные парадоксы в повседневной жизни.
Проблемный вопрос (вопрос для исследования)
Как вероятностные парадоксы влияют на повседневную жизнь?
Гипотеза исследования
Мы считаем,что зная некоторые понятия и аксиомы теории вероятности можно объяснить ситуации из реальной жизни, которые кажутся необъяснимыми человеку.
Цели исследования
- Провести опрос среди одноклассников о знаниях использования теории вероятности в реальной жизни.
- Установить связь парадоксов теории вероятности с реальной жизнью.
- Найти объяснение каждому парадоксу.
- Сделать выводы о проделанной работе.
Результаты проведённого исследования
1. Учащиеся видят непосредственную связь математики с окружающей действительностью, реальной жизнью, но не умеют применять это на практике. Поэтому мы решили провести опрос, чтобы выявить уровень их ориентированности в данной теме. В ходе опроса было видно, что ребятам интересна данная тема. В результате было выявлено, что учащиеся часто встречаются с парадоксами теории вероятности, но не знают, как это происходит. Следовательно, не могут применить их в жизни.
2. Выводы теории вероятностей находят применение в повседневной жизни, науке, технике и т.д. В повседневной жизни нам постоянно приходится сталкиваться со случайностью, и теория вероятностей учит нас, как действовать рационально с учетом риска, связанного с принятием отдельных решений. Современный образованный человек независимо от профессии и рода занятий должен быть знаком с простейшими понятиями теории вероятностей. В наши дни, когда прогноз погоды содержит сообщение о вероятности дождя на завтра, каждый должен знать что собственно это означает. Возьмем, к примеру, игру в монету. При бросании может быть два равновероятных исхода: монета может упасть кверху гербом или решкой. Бросая монету один раз нельзя предугадать, какая сторона окажется сверху. Однако, бросив монету 100 раз, можно сделать выводы. Можно заранее сказать, что герб выпадет не 1 и не 2 раза, а больше, но и не 99 и не 98 раз, а меньше. Число выпадений герба будет близко к 50. На самом деле, и на опыте можно в этом убедиться, что это число будет заключено между 40 и 60. Области применения теории вероятности
3. В ходе работы были рассмотрены два типа парадоксов. В теории вероятностей парадоксы бывают двух типов: первый — когда существует строгое решение в рамках аксиоматики, просто оно не очевидно, и условия задачи таковы, что ведут интуитивное понимание условий в ошибочном ключе, примерами таких парадоксов являются — парадокс игры в кости, Санкт-Петербургский парадокс, Парадокс закона больших чисел Бернулли, Парадокс раздачи подарков; второй тип — парадоксы, которые основываются на неоднозначной интерпретации аксиоматики теории вероятности, её недоопределённости, которую отмечал еще Пуанкаре, их и можно назвать истинными парадоксами. Примеры истинных парадоксов: Проблема Монти Холла, Парадокс мальчика и девочки. Ценность обоих типов парадоксов в том, что они помогают лучше понять суть теории, область её ограничения, глубже понять основания теории, и иногда исследование парадоксов вело к созданию отдельных разделов математики.
4.В результате проведенного исследования мы рассмотрели основные парадоксы теории вероятности, нашли обоснование для каждого парадокса и выяснили как они используются в реальной жизни. Наше знакомство с очень своеобразной областью математики, где между черным и белым существует целый спектр цветов и оттенков, возможностей и вариантов, а между однозначными «да» и «нет» существует еще и «быть может» (причем это «может быть» поддается строгой количественной оценке), способствует устранению укоренившегося ощущения, что происходящее на уроке математики никак не связано с окружающим миром, с повседневной жизнью. Мы увидели непосредственную связь математики с окружающей действительностью.
Вывод
В ходе исследования, гипотеза оказалась верна лишь частично, так как теория вероятности не может предсказывать исход абсолютно всех событий, а лишь некоторых. Но теория вероятности действительно может нам помочь, ведь, подсчитав по формуле, свои шансы, мы можем понять стоит ли делать что-то или нет. А без теории вероятности мы бы чаще ошибались, пробуя все подряд. Таким образом, зная теорию вероятности можно объяснить некоторые события нашей жизни. Благодаря теории вероятности, мы уменьшаем наши шансы на ошибку. И всегда лучше сначала узнать какова вероятность успеха, прежде чем делать. '
Полезные ресурсы
- Парадоксы теории вероятности
- Программа по созданию ментальных карт
- Создание диаграмм
- Как создать диаграмму
- Правила работы в Вики