Результаты исследований группы Историки в проекте Вычисляем рассуждения: различия между версиями
(→Результаты исследования) |
м (→Результаты исследования) |
||
| (не показано 46 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
==Название проекта== | ==Название проекта== | ||
| Строка 6: | Строка 5: | ||
==Авторы и участники проекта== | ==Авторы и участники проекта== | ||
*[[Участник:Никитаева Елена|Никитаева Елена Сергеевна]] : поиск и обработка информации | *[[Участник:Никитаева Елена|Никитаева Елена Сергеевна]] : поиск и обработка информации | ||
| − | *[[Участник:Kristina R|Родионова Кристина Владимировна]] : поиск и обработка информации | + | *[[Участник:Kristina R|Родионова Кристина Владимировна]], координатор : поиск и обработка информации |
| − | *[[Участник:Тумасов Иван Александрович|Тумасов Иван Александрович]] : создание Google Группы | + | *[[Участник:Тумасов Иван Александрович|Тумасов Иван Александрович]] : создание Google Группы, работа в wiki-портале |
| − | *[[Участник:Румянцева Анна|Румянцева Анна Сергеевна]] : работа с | + | *[[Участник:Румянцева Анна|Румянцева Анна Сергеевна]] : работа с картинками, создание ленты времени |
*[[Участник:Александр Овчинников ИСТ-10|Александр Овчинников]] : создание презентации | *[[Участник:Александр Овчинников ИСТ-10|Александр Овчинников]] : создание презентации | ||
*[[Участник:Мартынов Александр|Мартынов Александр]] : создание презентации | *[[Участник:Мартынов Александр|Мартынов Александр]] : создание презентации | ||
==Тема исследования группы== | ==Тема исследования группы== | ||
| − | + | Исторические предпосылки возникновения математической логики как науки. | |
== Проблемный вопрос (вопрос для исследования)== | == Проблемный вопрос (вопрос для исследования)== | ||
| Строка 26: | Строка 25: | ||
==Ход работы== | ==Ход работы== | ||
| − | + | ||
| − | + | [[Изображение:проект.JPG|500px]] | |
| − | |||
==Результаты исследования== | ==Результаты исследования== | ||
| + | Для организации взаимодействия в ходе проектной деятельности нами была создана | ||
[http://groups.google.ru/group/ist10istoriki'''Google группа'''] | [http://groups.google.ru/group/ist10istoriki'''Google группа'''] | ||
| + | Была организована совместная подборка ссылок по теме исследования с помощью [http://bobrdobr.ru/group/4083754/ '''сервиса БобрДобр'''] | ||
| − | ''' | + | '''ИСТОРИЯ ЛОГИКИ''' |
''Единственное средство улучшить наши умозаключения состоит в том, чтобы сделать их столь же наглядными, как и у математиков, - такими, что их ошибочность можно было бы увидеть глазами, и если между людьми возникают разногласия, достаточно было бы только сказать "Вычислим!", чтобы без дальнейших околичностей стало ясно, кто прав.'' | ''Единственное средство улучшить наши умозаключения состоит в том, чтобы сделать их столь же наглядными, как и у математиков, - такими, что их ошибочность можно было бы увидеть глазами, и если между людьми возникают разногласия, достаточно было бы только сказать "Вычислим!", чтобы без дальнейших околичностей стало ясно, кто прав.'' | ||
| − | '''Г.В. Лейбниц''' | + | [http://ru.wikipedia.org/wiki/%D0%9B%D0%B5%D0%B9%D0%B1%D0%BD%D0%B8%D1%86,_%D0%93%D0%BE%D1%82%D1%84%D1%80%D0%B8%D0%B4_%D0%92%D0%B8%D0%BB%D1%8C%D0%B3%D0%B5%D0%BB%D1%8C%D0%BC'''Г.В. Лейбниц'''] |
| + | |||
| + | Логика (от греч. “логос”, означающего “слово” и “смысл”) — одна из древнейших наук. Наука о законах, формах и операциях правильного мышления. Ее основная задача заключается в нахождении и систематизации правильных способов рассуждения.Кто, когда и где впервые обратился к тем аспектам мышления, которые составляют предмет логики, точно установить в настоящее время не представляется возможным. | ||
| + | |||
| + | Отдельные истоки логического учения можно обнаружить еще в Индии, в конце II тысячелетия до н.э. Логика как наука о мышлении первоначально возникает в связи с развитием практики ораторского искусства, как часть теории риторики. Такой характер носят истоки логики в Древней Индии, Древнем Китае, Древней Греции и Риме. В России первая оригинальная система логики, принадлежащая [http://rusnauka.narod.ru/lib/lomonosov_m/lomonosov.htm'''М. В. Ломоносову'''], изложена в его руководстве по теории красноречия. Таким образом, вначале логика выступает как одно из средств воздействия на умы людей, убеждения их в целесообразности того или иного поведения. В искусстве красноречия логический момент выступает еще как подчиненный, поскольку логические приемы служат не столько цели достижения истины, сколько цели убеждения аудитории. | ||
| + | |||
| + | Однако если говорить о возникновении логики как науки, то есть более или менее систематизированной совокупности знаний, то справедливым будет считать родиной логики великую цивилизацию Древней Греции. Именно здесь в V—IV веках до н. э. в период бурного развития демократии и связанного с ним небывалого оживления общественно-политической жизни трудами [http://teka.rus-impulse.ru/%D0%BF%D0%B0%D1%80%D0%BC%D0%B5%D0%BD%D0%B8%D0%B4 '''Парменида'''], [http://ru.wikipedia.org/wiki/%D0%A1%D0%BE%D0%BA%D1%80%D0%B0%D1%82 '''Сократа'''],[http://fictionbook.ru/author/d_a_shadrin/logika_konspekt_lekciyi/read_online.html?page=1'''Платона'''] и [http://www.krugosvet.ru/enc/gumanitarnye_nauki/filosofiya/ZENON_ELESKI.html'''Зенона'''] [http://bluesky.ua/Turciya-t130/<span style="color:black;font-weight:normal; text-decoration:none!important; background:none!important; text-decoration:none;">путевки в Турцию</span>] были заложены основы этой науки. В Древней Индии и Китае историческое развитие логики тесно связано с именами таких философов и мыслителей, как Нагарджуна, [http://www.gumfak.ru/filos_html/kratk_filos/hist06.shtml'''Акшапада Гаутама'''] и [http://china.aforism.ru/html/mo-czi/00001.htm'''Мо-Цзы''']. Родоначальником же, «отцом» логики, по праву считается величайший мыслитель древности, ученик Платона — [http://www.physchem.chimfak.rsu.ru/Source/History/Persones/Aristoteles.html'''Аристотель'''](384—322 гг. до н. э.). | ||
| + | |||
| + | '''Логика в Древней Греции''' | ||
| + | |||
| + | [[Изображение:парменид.JPG|100px]] | ||
| − | + | '''''Парменид''''' (540 – 450 гг. до н.э.) - древнегреческий философ и мыслитель из Элеи, представитель элейской школы. Помимо философии, занимался законодательством. Существо философской логической позиции Парменида заключается в проведении принципиального различия между мышлением и чувственностью, а соответственно и между мыслимым миром и миром чувственно познаваемым. Парменид даёт одну из первых формулировок идеи тождества бытия и мышления: «мыслить и быть есть одно и то же», «одно и то же мысль и то, на что мысль устремляется». Такое бытие, по Пармениду, никогда не может быть небытием, поскольку последнее — это нечто слепое и непознаваемое; бытие не может ни происходить из небытия, ни каким-либо образом содержать его в себе. Вопреки сложившемуся ещё в древности мнению, Парменид вовсе не отрицал чувственного мира, а только доказывал, что для его философского и научного осознания мало одной чувственности. Считая критерием истины разум, он отвергал ощущения из-за их неточности. Чувственный мир Парменид трактовал в духе ранней греческой натурфилософии как смешение огня и земли, светлого и тёмного, тёплого и холодного, тонкого и плотного, лёгкого и тяжёлого. | |
| − | |||
| − | ''' | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Есть мыслители одной фразы которых всем прочим хватает на тысячелетия. У Парменида такая фраза есть: «Одно и то же – внимать (мыслить) и быть». Мышление и его возможности для Парменида являются критериями истинности. Логика, идущая от Парменида демонстрирует, что возможности делающего больше, чем мыслящего. И с этим приходится считаться. | |
| − | |||
| − | |||
| − | + | [[Изображение:сократ.JPG|100px]] | |
| − | + | ||
| − | + | '''''Сократ''''' (ок.469 - 399 гг.до н. э.) — древнегреческий философ, учение которого знаменует поворот в философии — от рассмотрения природы и мира к рассмотрению человека. Приговорён к смерти за «развращение молодежи» и «непочитание богов». Его деятельность — поворотный момент античной философии. Своим методом анализа понятий и отождествлением добродетели и знания он направил внимание философов на безусловное значение человеческой личности. Сократ излагал свои мысли в устной форме, в разговорах с разными лицами; до нас дошли сведения о содержании этих разговоров в сочинениях его учеников, Платона и Ксенофонта. Его вклад в развитие логики того времени заключается в особых методах, подходах к поиску истинных суждений. Вот один из них – так называемый «сократический метод»: Своих учеников Сократ приводил к истинному суждению через диалог, где задавал общий вопрос, получив ответ, задавал следующий уточняющий вопрос и так далее до окончательного ответа. | |
| − | + | ||
| − | + | [[Изображение:платон.JPG|100px]] | |
| − | + | ||
| − | + | '''''Платон''''' (428 – 348 гг.до н.э.) - древнегреческий философ. Ученик Сократа. Он разрабатывал теории познания и логики, опираясь на идеи учителя. Используя свои теории, Платон сначала получал новые понятия, а затем старался разбить их на виды и систематизировать.Для этого он использовал свой излюбленный прием под названием «дихотомия», т.е. деление понятия А на В и не В (например, преступления могут быть умышленными и неумышленными, а животные позвоночными или беспозвоночными). Как и в школе Сократа, ученики Академии Платона много занимались получением новых определений. | |
| − | + | ||
| + | Платон развивал теорию суждения, создал два правила деления понятий, а также отличал отношение различия от отношения противоположности. | ||
| + | Необходимо упомянуть о [http://www.gumer.info/bogoslov_Buks/Philos/fil_dict/763.php'''логике стоиков'''] – системе знаний, разработанных приверженцами мегаро-стоической школы, стоиками Зеноном и [http://dic.academic.ru/dic.nsf/enc_philosophy/1337/%D0%A5%D0%A0%D0%98%D0%A1%D0%98%D0%9F%D0%9F'''Хризиппом'''] и мегариками [http://slovari.yandex.ru/~%D0%BA%D0%BD%D0%B8%D0%B3%D0%B8/%D0%91%D0%A1%D0%AD/%D0%94%D0%B8%D0%BE%D0%B4%D0%BE%D1%80%20%D0%A1%D0%B8%D1%86%D0%B8%D0%BB%D0%B8%D0%B9%D1%81%D0%BA%D0%B8%D0%B9/'''Диодором'''], [http://ariom.ru/wiki/MegarskajaShkola/print'''Стилпоном'''], [http://ru.wikipedia.org/wiki/%D0%A4%D0%B8%D0%BB%D0%BE%D0%BD_%D0%90%D0%BB%D0%B5%D0%BA%D1%81%D0%B0%D0%BD%D0%B4%D1%80%D0%B8%D0%B9%D1%81%D0%BA%D0%B8%D0%B9'''Филоном'''] и [http://filpedia.ru/85/'''Евбулидом''']. В результате деятельности этой школы современная логика получила анализ логических понятий отрицания, конъюнкции, дизъюнкции и импликации. Задачей логики они видели избавление от заблуждений и создание возможности правильно судить о вещах. Логика должна изучать не только словесные знаки, но и мысли, выражающиеся в них. К сожалению, представления данной философской школы в области логики лишь частью дошли до нашего времени. | ||
| + | |||
| + | '''Логика в Древнем Китае''' | ||
| + | |||
| + | История свидетельствует, что отдельные логические проблемы возникают перед мысленным взором человека уже свыше 2,5 тыс. лет назад — сначала в Древней Индии и Древнем Китае, где большое внимание уделялось этическим, философским и политическим вопросам, которые закреплялись в большом количестве трактатов. | ||
| − | + | К философским школам, существовавшим в Китае на тот момент, можно отнести минцзя (школа имен), фацзя (школа законов), жуцзя (развивающая конфуцианские идеи) и моцзя (школа моистов). В результате деятельности этих школ постепенно стала складываться более-менее стройная система логики. Среди известных представителей философских учений, также развивающих идеи логики, можно назвать имя древнекитайского философа и мудреца - Мо-цзы (470 – 391 гг. до н.э.). Однако, поскольку логические знания были разобщены, закреплены не в одном источнике, а во многих трактатах, они требовали систематизации. Необходима была школа, которая бы объединила все знания о логике в едином акте, что значительно бы упростило использование логических достижений. Такой школой стала школа моцзя. Поздние моисты, используя философию Мо-цзы, создали первый в Китае трактат по логике под названием «Мобянь». | |
| − | + | Китай всегда был очень самобытной страной с богатой культурой, развитым общественным строем и жестким чувством подчинения. Мудрецы, старейшины всегда пользовались известными привилегиями. Такое положение не могло не отразиться на логике Древнего Китая. Сильное влияние на логические теории здесь оказывали политические и этические доктрины, а сама логика носила характер прикладной и использовалась для достижения риторических целей. Поэтому практически не было выведено четкой системы знаний об умозаключениях. Предпочтение перед формой отдавалось содержанию мышления. В результате, хотя логика в Древнем Китае и возникла по времени раньше, чем древнегреческая, ее структура так и не была выстроена и осталась в зачаточном состоянии. | |
| + | |||
| + | '''Логика в Древней Индии''' | ||
| + | |||
| + | Истоки логики в Индии можно проследить в грамматических текстах V века до н. э.. Две из шести ортодоксально-индуистских (ведийских) школ индийской философии — [http://ru.wikipedia.org/wiki/%D0%9D%D1%8C%D1%8F%D1%8F'''ньяя и вайшешика'''] — занимались методологией познания, из этого проблемного поля и выделилась логика. | ||
| − | + | Само название школы «ньяя» значит «логика». Главным её достижением и была разработка логики и методологии, ставших впоследствии общим достоянием (аристотелевская логика в Европе). Основным текстом школы были Ньяя - [http://ru.wikipedia.org/wiki/%D0%9D%D1%8C%D1%8F%D1%8F-%D1%81%D1%83%D1%82%D1%80%D1%8B'''сутры Акшапады Гаутамы'''] (II век н. э.). Поскольку ньяики считали единственным путём освобождения от страданий достижение надёжного знания, они разрабатывали тонкие методы отличения надёжных источников знания от ложных мнений. Есть только четыре источника знания (четыре праманы): восприятие, умозаключение, сравнение и свидетельство. Строгая пятичленная схема умозаключения включала в себя: начальную посылку, основание, пример, приложение и вывод. | |
| − | + | ||
| − | + | Буддийская философия (не входившая в число шести ортодоксальных школ) была главным оппонентом ньяиков в логике.[http://ru.wikipedia.org/wiki/%D0%9D%D0%B0%D0%B3%D0%B0%D1%80%D0%B4%D0%B6%D1%83%D0%BD%D0%B0'''Нагарджуна'''], основатель [http://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D0%B4%D1%85%D1%8A%D1%8F%D0%BC%D0%B0%D0%BA%D0%B0'''мадхьямики'''] («срединного пути»,одного из двух направлений философского буддизма), развил рассуждение, известное как «катускоти», или тетралемма. Этот четырёхсторонний аргумент систематически проверял и отклонял утверждение высказывания, его отрицание, соединение утверждения и отрицания и, наконец, отклонение и его утверждения, и его отрицания. | |
| − | + | У выдающегося индийского мыслителя [http://ru.wikipedia.org/wiki/%D0%94%D0%B8%D0%B3%D0%BD%D0%B0%D0%B3%D0%B0'''Дигнаги'''] и его последователя [http://ru.wikipedia.org/wiki/%D0%94%D1%85%D0%B0%D1%80%D0%BC%D0%B0%D0%BA%D0%B8%D1%80%D1%82%D0%B8'''Дхармакирти'''] буддийская логика достигла вершины. Центральным пунктом их анализа было установление (определение) необходимой логической присущности (включённости в определение), «вьяпти», также известное как «неизменное следование» или «убеждение». Для этой цели они развили учение об «апоха» или различении, о правилах включения признаков в определение или исключения их из него. | |
| − | В | + | |
| − | + | Школа навья-ньяя («новая ньяя», «новая логика») была основана в XIII веке Ганешей Упадхьяей из Митилы, автора «Таттвачинтамами» («Сокровище мысли о реальности»). Впрочем, он и опирался на работы своих предшественников X века. | |
| − | + | ||
| − | + | В настоящее время логика представляет собой весьма разветвленную и многоплановую науку, результаты и методы которой активно используются во многих областях теоретического познания, в том числе и непосредственно связанных с рядом современных направлений практической деятельности. Она находит применение в философии, математике, психологии, кибернетике, лингвистике и др. | |
| − | ''''' | + | |
| + | Результаты нашего исследования по темам формальной и математической логики мы отразили в виде презентаций: | ||
| + | |||
| + | [https://docs.google.com/fileview?id=0B491l8vmqrNqODdjNTlhMWYtMDYwNS00ODU1LThjYjMtN2Y4ZGRmZDBlOTVh&hl=ru'''История формальной логики'''] | ||
| + | |||
| + | [https://docs.google.com/fileview?id=0B491l8vmqrNqMTQyMmEwNjItMDRlNy00ODUwLWFiMmItNzI4OGMyNzI0Y2Jj&hl=ru'''История математической логики'''] | ||
| − | + | Завершаем наше исследование лентой времени: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Изображение:Для Историков из Ист-10.JPG|800px]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Вывод== | ==Вывод== | ||
| + | В результате работы над проектом мы утвердились в мысли, что появление '''современной математической логики''' является наиболее значительным событием в истории логики за последние две тысячи лет и, возможно, одним из наиболее важных и примечательных событий в интеллектуальной истории человечества. | ||
==Полезные ресурсы== | ==Полезные ресурсы== | ||
| Строка 117: | Строка 104: | ||
[http://logic.vbelous.net/cl-logic/beginning.htm'''Начало науки о рассуждениях'''] | [http://logic.vbelous.net/cl-logic/beginning.htm'''Начало науки о рассуждениях'''] | ||
| + | |||
| + | [http://ru.wikipedia.org/wiki/%D0%9B%D0%BE%D0%B3%D0%B8%D0%BA%D0%B0'''История логики'''] | ||
| + | |||
| + | [http://psychology.filolingvia.com/publ/44-1-0-324'''История развития логики'''] | ||
| + | |||
| + | [http://fictionbook.ru/author/d_a_shadrin/logika_konspekt_lekciyi/read_online.html?page=1'''Древние истоки логики'''] | ||
| + | |||
| + | [http://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D0%BB%D0%BE%D0%B3%D0%B8%D0%BA%D0%B0'''Математическая логика'''] | ||
| + | |||
| + | [http://www.ido.rudn.ru/nfpk/inf/inf7.html'''Математическая логика в информатике'''] | ||
| + | |||
| + | [http://filosof.historic.ru/enc/item/f00/s12/a001217.shtml'''Формальная логика'''] | ||
== Другие документы == | == Другие документы == | ||
[[Категория:Проекты]] | [[Категория:Проекты]] | ||
Текущая версия на 16:59, 25 апреля 2012
Содержание
Название проекта
Учебный проект Вычисляем рассуждения
Авторы и участники проекта
- Никитаева Елена Сергеевна : поиск и обработка информации
- Родионова Кристина Владимировна, координатор : поиск и обработка информации
- Тумасов Иван Александрович : создание Google Группы, работа в wiki-портале
- Румянцева Анна Сергеевна : работа с картинками, создание ленты времени
- Александр Овчинников : создание презентации
- Мартынов Александр : создание презентации
Тема исследования группы
Исторические предпосылки возникновения математической логики как науки.
Проблемный вопрос (вопрос для исследования)
Как возникла идея перевода рассуждений на математический язык?
Гипотеза исследования
Мы считаем, что предпосылкой возникновения математической логики как науки является стремление ученых представить человеческие рассуждения на языке математики, чтобы можно было вычислить их истинность.
Цель исследования
Осуществить поиск и провести анализ исторических фактов о предпосылках возникновения математической логики.
Ход работы
Результаты исследования
Для организации взаимодействия в ходе проектной деятельности нами была создана Google группа
Была организована совместная подборка ссылок по теме исследования с помощью сервиса БобрДобр
ИСТОРИЯ ЛОГИКИ
Единственное средство улучшить наши умозаключения состоит в том, чтобы сделать их столь же наглядными, как и у математиков, - такими, что их ошибочность можно было бы увидеть глазами, и если между людьми возникают разногласия, достаточно было бы только сказать "Вычислим!", чтобы без дальнейших околичностей стало ясно, кто прав.
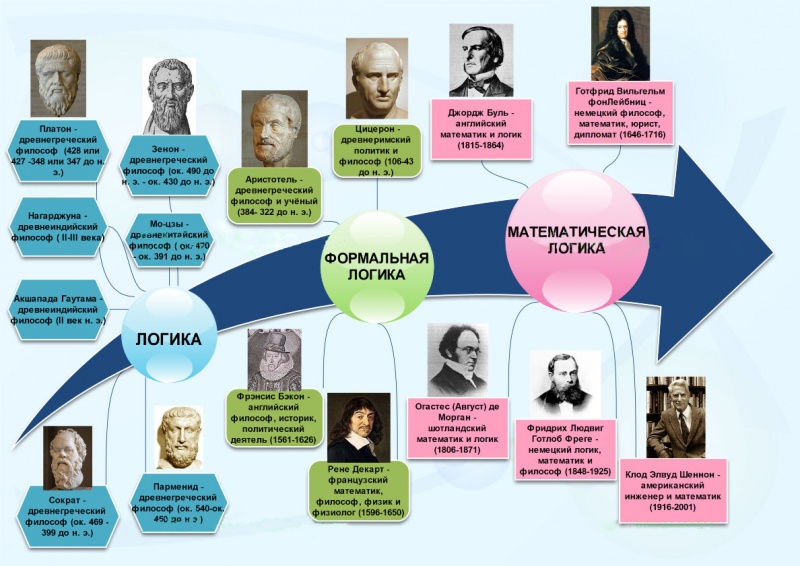
Логика (от греч. “логос”, означающего “слово” и “смысл”) — одна из древнейших наук. Наука о законах, формах и операциях правильного мышления. Ее основная задача заключается в нахождении и систематизации правильных способов рассуждения.Кто, когда и где впервые обратился к тем аспектам мышления, которые составляют предмет логики, точно установить в настоящее время не представляется возможным.
Отдельные истоки логического учения можно обнаружить еще в Индии, в конце II тысячелетия до н.э. Логика как наука о мышлении первоначально возникает в связи с развитием практики ораторского искусства, как часть теории риторики. Такой характер носят истоки логики в Древней Индии, Древнем Китае, Древней Греции и Риме. В России первая оригинальная система логики, принадлежащая М. В. Ломоносову, изложена в его руководстве по теории красноречия. Таким образом, вначале логика выступает как одно из средств воздействия на умы людей, убеждения их в целесообразности того или иного поведения. В искусстве красноречия логический момент выступает еще как подчиненный, поскольку логические приемы служат не столько цели достижения истины, сколько цели убеждения аудитории.
Однако если говорить о возникновении логики как науки, то есть более или менее систематизированной совокупности знаний, то справедливым будет считать родиной логики великую цивилизацию Древней Греции. Именно здесь в V—IV веках до н. э. в период бурного развития демократии и связанного с ним небывалого оживления общественно-политической жизни трудами Парменида, Сократа,Платона и Зенона путевки в Турцию были заложены основы этой науки. В Древней Индии и Китае историческое развитие логики тесно связано с именами таких философов и мыслителей, как Нагарджуна, Акшапада Гаутама и Мо-Цзы. Родоначальником же, «отцом» логики, по праву считается величайший мыслитель древности, ученик Платона — Аристотель(384—322 гг. до н. э.).
Логика в Древней Греции
Парменид (540 – 450 гг. до н.э.) - древнегреческий философ и мыслитель из Элеи, представитель элейской школы. Помимо философии, занимался законодательством. Существо философской логической позиции Парменида заключается в проведении принципиального различия между мышлением и чувственностью, а соответственно и между мыслимым миром и миром чувственно познаваемым. Парменид даёт одну из первых формулировок идеи тождества бытия и мышления: «мыслить и быть есть одно и то же», «одно и то же мысль и то, на что мысль устремляется». Такое бытие, по Пармениду, никогда не может быть небытием, поскольку последнее — это нечто слепое и непознаваемое; бытие не может ни происходить из небытия, ни каким-либо образом содержать его в себе. Вопреки сложившемуся ещё в древности мнению, Парменид вовсе не отрицал чувственного мира, а только доказывал, что для его философского и научного осознания мало одной чувственности. Считая критерием истины разум, он отвергал ощущения из-за их неточности. Чувственный мир Парменид трактовал в духе ранней греческой натурфилософии как смешение огня и земли, светлого и тёмного, тёплого и холодного, тонкого и плотного, лёгкого и тяжёлого.
Есть мыслители одной фразы которых всем прочим хватает на тысячелетия. У Парменида такая фраза есть: «Одно и то же – внимать (мыслить) и быть». Мышление и его возможности для Парменида являются критериями истинности. Логика, идущая от Парменида демонстрирует, что возможности делающего больше, чем мыслящего. И с этим приходится считаться.
Сократ (ок.469 - 399 гг.до н. э.) — древнегреческий философ, учение которого знаменует поворот в философии — от рассмотрения природы и мира к рассмотрению человека. Приговорён к смерти за «развращение молодежи» и «непочитание богов». Его деятельность — поворотный момент античной философии. Своим методом анализа понятий и отождествлением добродетели и знания он направил внимание философов на безусловное значение человеческой личности. Сократ излагал свои мысли в устной форме, в разговорах с разными лицами; до нас дошли сведения о содержании этих разговоров в сочинениях его учеников, Платона и Ксенофонта. Его вклад в развитие логики того времени заключается в особых методах, подходах к поиску истинных суждений. Вот один из них – так называемый «сократический метод»: Своих учеников Сократ приводил к истинному суждению через диалог, где задавал общий вопрос, получив ответ, задавал следующий уточняющий вопрос и так далее до окончательного ответа.
Платон (428 – 348 гг.до н.э.) - древнегреческий философ. Ученик Сократа. Он разрабатывал теории познания и логики, опираясь на идеи учителя. Используя свои теории, Платон сначала получал новые понятия, а затем старался разбить их на виды и систематизировать.Для этого он использовал свой излюбленный прием под названием «дихотомия», т.е. деление понятия А на В и не В (например, преступления могут быть умышленными и неумышленными, а животные позвоночными или беспозвоночными). Как и в школе Сократа, ученики Академии Платона много занимались получением новых определений.
Платон развивал теорию суждения, создал два правила деления понятий, а также отличал отношение различия от отношения противоположности. Необходимо упомянуть о логике стоиков – системе знаний, разработанных приверженцами мегаро-стоической школы, стоиками Зеноном и Хризиппом и мегариками Диодором, Стилпоном, Филоном и Евбулидом. В результате деятельности этой школы современная логика получила анализ логических понятий отрицания, конъюнкции, дизъюнкции и импликации. Задачей логики они видели избавление от заблуждений и создание возможности правильно судить о вещах. Логика должна изучать не только словесные знаки, но и мысли, выражающиеся в них. К сожалению, представления данной философской школы в области логики лишь частью дошли до нашего времени.
Логика в Древнем Китае
История свидетельствует, что отдельные логические проблемы возникают перед мысленным взором человека уже свыше 2,5 тыс. лет назад — сначала в Древней Индии и Древнем Китае, где большое внимание уделялось этическим, философским и политическим вопросам, которые закреплялись в большом количестве трактатов.
К философским школам, существовавшим в Китае на тот момент, можно отнести минцзя (школа имен), фацзя (школа законов), жуцзя (развивающая конфуцианские идеи) и моцзя (школа моистов). В результате деятельности этих школ постепенно стала складываться более-менее стройная система логики. Среди известных представителей философских учений, также развивающих идеи логики, можно назвать имя древнекитайского философа и мудреца - Мо-цзы (470 – 391 гг. до н.э.). Однако, поскольку логические знания были разобщены, закреплены не в одном источнике, а во многих трактатах, они требовали систематизации. Необходима была школа, которая бы объединила все знания о логике в едином акте, что значительно бы упростило использование логических достижений. Такой школой стала школа моцзя. Поздние моисты, используя философию Мо-цзы, создали первый в Китае трактат по логике под названием «Мобянь».
Китай всегда был очень самобытной страной с богатой культурой, развитым общественным строем и жестким чувством подчинения. Мудрецы, старейшины всегда пользовались известными привилегиями. Такое положение не могло не отразиться на логике Древнего Китая. Сильное влияние на логические теории здесь оказывали политические и этические доктрины, а сама логика носила характер прикладной и использовалась для достижения риторических целей. Поэтому практически не было выведено четкой системы знаний об умозаключениях. Предпочтение перед формой отдавалось содержанию мышления. В результате, хотя логика в Древнем Китае и возникла по времени раньше, чем древнегреческая, ее структура так и не была выстроена и осталась в зачаточном состоянии.
Логика в Древней Индии
Истоки логики в Индии можно проследить в грамматических текстах V века до н. э.. Две из шести ортодоксально-индуистских (ведийских) школ индийской философии — ньяя и вайшешика — занимались методологией познания, из этого проблемного поля и выделилась логика.
Само название школы «ньяя» значит «логика». Главным её достижением и была разработка логики и методологии, ставших впоследствии общим достоянием (аристотелевская логика в Европе). Основным текстом школы были Ньяя - сутры Акшапады Гаутамы (II век н. э.). Поскольку ньяики считали единственным путём освобождения от страданий достижение надёжного знания, они разрабатывали тонкие методы отличения надёжных источников знания от ложных мнений. Есть только четыре источника знания (четыре праманы): восприятие, умозаключение, сравнение и свидетельство. Строгая пятичленная схема умозаключения включала в себя: начальную посылку, основание, пример, приложение и вывод.
Буддийская философия (не входившая в число шести ортодоксальных школ) была главным оппонентом ньяиков в логике.Нагарджуна, основатель мадхьямики («срединного пути»,одного из двух направлений философского буддизма), развил рассуждение, известное как «катускоти», или тетралемма. Этот четырёхсторонний аргумент систематически проверял и отклонял утверждение высказывания, его отрицание, соединение утверждения и отрицания и, наконец, отклонение и его утверждения, и его отрицания. У выдающегося индийского мыслителя Дигнаги и его последователя Дхармакирти буддийская логика достигла вершины. Центральным пунктом их анализа было установление (определение) необходимой логической присущности (включённости в определение), «вьяпти», также известное как «неизменное следование» или «убеждение». Для этой цели они развили учение об «апоха» или различении, о правилах включения признаков в определение или исключения их из него.
Школа навья-ньяя («новая ньяя», «новая логика») была основана в XIII веке Ганешей Упадхьяей из Митилы, автора «Таттвачинтамами» («Сокровище мысли о реальности»). Впрочем, он и опирался на работы своих предшественников X века.
В настоящее время логика представляет собой весьма разветвленную и многоплановую науку, результаты и методы которой активно используются во многих областях теоретического познания, в том числе и непосредственно связанных с рядом современных направлений практической деятельности. Она находит применение в философии, математике, психологии, кибернетике, лингвистике и др.
Результаты нашего исследования по темам формальной и математической логики мы отразили в виде презентаций:
Завершаем наше исследование лентой времени:
Вывод
В результате работы над проектом мы утвердились в мысли, что появление современной математической логики является наиболее значительным событием в истории логики за последние две тысячи лет и, возможно, одним из наиболее важных и примечательных событий в интеллектуальной истории человечества.
Полезные ресурсы
Математическая логика. Предмет и история развития
Математическая логика в информатике