Результаты исследований обучающихся в проекте Искусство в математике: различия между версиями
(→Результаты проведённого исследования) |
(→Полезные ресурсы) |
||
| (не показано 11 промежуточных версий этого же участника) | |||
| Строка 47: | Строка 47: | ||
Первое - это цифровые обозначения. Как и в математике, в музыке встречаются цифры: звукоряд – 7 нот, нотный стан – 5 линеек. Интервалы: прима – 1, секунда – 2, терция – 3, кварта – 4, квинта – 5, секста – 6, септима – 7, октава – 8. Обозначения аппликатуры и размер произведения записывается тоже при помощи цифр. | Первое - это цифровые обозначения. Как и в математике, в музыке встречаются цифры: звукоряд – 7 нот, нотный стан – 5 линеек. Интервалы: прима – 1, секунда – 2, терция – 3, кварта – 4, квинта – 5, секста – 6, септима – 7, октава – 8. Обозначения аппликатуры и размер произведения записывается тоже при помощи цифр. | ||
| − | Второе совпадение – это ритм. Ритм важнейший элемент в музыке. У каждого музыкального произведения свой ритмический рисунок (чередование нот разной длительности). Числа, оказывается, тоже обладают ритмом. | + | Второе совпадение – это [https://ru.wikipedia.org/wiki/%D0%A0%D0%B8%D1%82%D0%BC ритм]. Ритм важнейший элемент в музыке. У каждого музыкального произведения свой ритмический рисунок (чередование нот разной длительности). Числа, оказывается, тоже обладают ритмом. |
Например, числа кратные 3(трём) обладают следующим ритмом: Начнем с 0 и, увеличивая каждый раз на 1, будем акцентировать все числа, кратные 3. Получается 0 1 2 3 4 5 6 7 8…. и т.д. Получается красивый, правильный, равномерный ритм, звучащий как музыкальный размер 3/4, который соответствует вальсу. | Например, числа кратные 3(трём) обладают следующим ритмом: Начнем с 0 и, увеличивая каждый раз на 1, будем акцентировать все числа, кратные 3. Получается 0 1 2 3 4 5 6 7 8…. и т.д. Получается красивый, правильный, равномерный ритм, звучащий как музыкальный размер 3/4, который соответствует вальсу. | ||
| Строка 71: | Строка 71: | ||
|} | |} | ||
| − | Четвертое совпадение | + | Четвертое совпадение мы обнаружили при изучении темы по математике [https://ru.wikipedia.org/wiki/%D0%94%D1%80%D0%BE%D0%B1%D1%8C_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0) «Дроби»]. Мы знаем, что в целой ноте - две половинных, четыре четвертных, восемь восьмых, 16 шестнадцатых. Оказывается, что длительности получаются так же, как и дроби: они возникают при делении целой на равные доли. Поэтому длительность можно подсчитывать так же как дробные числа: 1/2, ¼, 1/8, 1/16. Следовательно, названия длительностей служат одновременно и названиями чисел. |
| − | Пятое совпадение - в музыке, как и в математике, есть понятие параллельности. Это - параллельные тональности (например, до мажор – ля минор), а ещё линии нотного стана всегда параллельны, то есть, никогда не пересекаются. | + | Пятое совпадение - в музыке, как и в математике, есть понятие параллельности. Это - [https://ru.wikipedia.org/wiki/%D0%9F%D0%B0%D1%80%D0%B0%D0%BB%D0%BB%D0%B5%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5_%D1%82%D0%BE%D0%BD%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D1%81%D1%82%D0%B8 параллельные тональности] (например, до мажор – ля минор), а ещё линии нотного стана всегда параллельны, то есть, никогда не пересекаются. |
| − | Таким образом, | + | Таким образом, мы установили 5 совпадений музыки с математикой, из чего можно сделать вывод, что занимаясь музыкой, человек развивает и тренирует свои математические способности. |
| + | |||
| + | Используя возможности всемирной паутины несложно было найти наглядное изображение тесной дружбы математики и музыки - музыкальную машину из дерева, которая производит звуки при помощи двух тысяч стальных шариков, сконструировали в Швеции. Авторами необычного и до сих пор не существовавшего музыкального инструмента стали участники музыкальной группы Wintergatan. | ||
| + | |||
| + | Стальные шарики небольшого размера - главный элемент в механизме, издающем мелодичные звуки. Внутри машины, на бобине, находится лента, которая задает основную мелодию. Все остальные элементы - это ударные и басы, которым можно задавать различный темп. | ||
| + | |||
| + | На постройку «музыкального механизма будущего», на расчет и постройку, по словам его создателей, ушло больше одного года. | ||
| + | |||
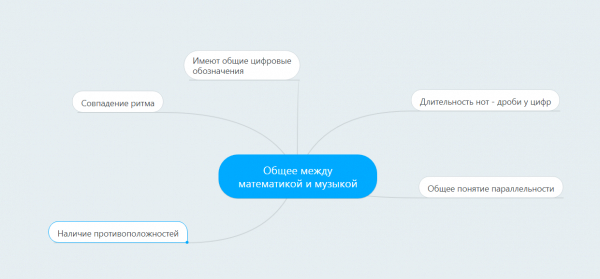
| + | [https://mm.tt/779938836?t=SXNv713b9J Ментальная карта] | ||
| + | |||
| + | [[ Изображение: Ментальная топорова.png | 600 px]] | ||
| + | |||
| + | [https://drive.google.com/open?id=1CugaXkCjXUB3IF5zDaxZR3PLYp6Vv0qt Презентация математика в музыке] | ||
==Вывод== | ==Вывод== | ||
| − | #В ходе исследования | + | #В ходе исследования удалось провести параллель между математикой и музыкой, установить между ними прямую связь; |
#Были получены результаты о том, как именно связаны цифры и ноты; | #Были получены результаты о том, как именно связаны цифры и ноты; | ||
#Выяснилось, в каких конкретно областях наблюдается непосредственная связь между гармоничным звучанием мелодии и четкой математической записью. | #Выяснилось, в каких конкретно областях наблюдается непосредственная связь между гармоничным звучанием мелодии и четкой математической записью. | ||
==Полезные ресурсы== | ==Полезные ресурсы== | ||
| + | |||
| + | [https://biblioclub.ru/index.php?page=book_red&id=131254&sr=1 Культура и искусство: поиски и открытия. Материалы межрегиональной научно-практической студенческой конференции (г. Кемерово, 23 апреля 2009 г.) / ред. В.И. Марков. - Кемерово : КемГУКИ, 2009. - 286 с] | ||
| + | |||
| + | [https://biblioclub.ru/index.php?page=book_red&id=494801&sr=1 Яшин, Б.Л. Философские проблемы математики: история и современность : монография / Б.Л. Яшин. - Москва ; Берлин : Директ-Медиа, 2018. - 210 с. - Библиогр. в кн.] | ||
| + | |||
| + | [https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0_%D0%B8_%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D0%B8%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D0%B8%D1%81%D0%BA%D1%83%D1%81%D1%81%D1%82%D0%B2%D0%BE Математика и изобразительное искусство Википедия] | ||
| + | |||
| + | [https://www.popmech.ru/science/8242-matematika-kak-iskusstvo-chto-skryvaetsya-za-tsiframi/ Популярная механика Математика как искусство: что скрывается за цифрами?] | ||
| + | |||
| + | [https://f.ua/mann-ivanov-i-ferber/krasota-v-kvadrate-kak-cifriy-otrajayut-jizn-i-jizn-otrajaet-cifriy_31494.html Красота в квадрате А. Беллос] | ||
| + | |||
| + | [http://mathemlib.ru/books/item/f00/s00/z0000011/index.shtml Волошинов А. В. Математика и искусство] | ||
== Другие документы == | == Другие документы == | ||
| + | [[Учебный проект Искусство в математике]] | ||
| + | |||
| + | [[Основной курс программы Intel Обучение для будущего МФ-16-1 май-июнь 2019]] | ||
[[Категория:Проекты]] | [[Категория:Проекты]] | ||
| − | |||
| − | |||
Текущая версия на 11:30, 24 июня 2019
Содержание
Авторы и участники проекта
Участник группы: Вольфганг Амадей Моцарт
Тема исследования группы
Связь математики и музыки
Проблемный вопрос (вопрос для исследования)
Существует ли связь между математикой и музыкой?
Гипотеза исследования
Мы считаем, что математика и искусство непосредственно связаны между собой, что для приятной слуху мелодии ноты должны быть выстроены в определенном порядке.
Цели исследования
- Доказать, что связь между музыкой и математикой существует;
- Выяснить, может ли математическая формула звучать красиво;
- Исследовать влияние математики на музыку и наоборот.
Результаты проведённого исследования
Математика в музыке.
- Математика (греч. - знание, наука). Математика – царица всех наук, символ мудрости. Красота математики является одним из связующих звеньев науки и искусства.
- Музыка (греч. – искусство муз), значит искусство, отражающее действительность в звуковых, художественных образах.
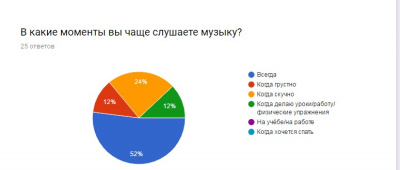
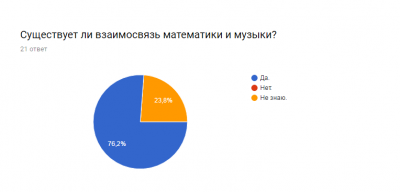
Перед началом исследования был проведен опрос на предмет присутствия музыки в жизни людей.
1.
2.
Из чего был сделан вывод о том, что музыка является важной составляющей повседневной жизни человека и большая половина опрошенных респондентов считает, что связь между математикой и музыкой существует достаточно сильная.
Из знаний, полученных на уроках по математике и занятий по музыке, я выявила следующие совпадения:
Первое - это цифровые обозначения. Как и в математике, в музыке встречаются цифры: звукоряд – 7 нот, нотный стан – 5 линеек. Интервалы: прима – 1, секунда – 2, терция – 3, кварта – 4, квинта – 5, секста – 6, септима – 7, октава – 8. Обозначения аппликатуры и размер произведения записывается тоже при помощи цифр.
Второе совпадение – это ритм. Ритм важнейший элемент в музыке. У каждого музыкального произведения свой ритмический рисунок (чередование нот разной длительности). Числа, оказывается, тоже обладают ритмом.
Например, числа кратные 3(трём) обладают следующим ритмом: Начнем с 0 и, увеличивая каждый раз на 1, будем акцентировать все числа, кратные 3. Получается 0 1 2 3 4 5 6 7 8…. и т.д. Получается красивый, правильный, равномерный ритм, звучащий как музыкальный размер 3/4, который соответствует вальсу.
Если посчитать числа, кратные двум 0 1 2 3 4 5 6 7 8 9 и т.д. то увидим, что мы пришли к ритму, звучащему, как музыкальный размер 2/4. Таким образом, числа обладают ритмом.
Третье совпадение – наличие в музыке и математике противоположностей.
| Музыка | Математика |
|---|---|
| Мажор-минор | Плюс-минус |
| Быстро-медленно | Больше-меньше |
| Тихо-громко | Сложение-вычитание |
| Низкий звук-высокий звук | Умножение-деление |
| Бемоль(повышение)-дизе(понижение) | Четное число - нечетное число |
Четвертое совпадение мы обнаружили при изучении темы по математике «Дроби». Мы знаем, что в целой ноте - две половинных, четыре четвертных, восемь восьмых, 16 шестнадцатых. Оказывается, что длительности получаются так же, как и дроби: они возникают при делении целой на равные доли. Поэтому длительность можно подсчитывать так же как дробные числа: 1/2, ¼, 1/8, 1/16. Следовательно, названия длительностей служат одновременно и названиями чисел.
Пятое совпадение - в музыке, как и в математике, есть понятие параллельности. Это - параллельные тональности (например, до мажор – ля минор), а ещё линии нотного стана всегда параллельны, то есть, никогда не пересекаются.
Таким образом, мы установили 5 совпадений музыки с математикой, из чего можно сделать вывод, что занимаясь музыкой, человек развивает и тренирует свои математические способности.
Используя возможности всемирной паутины несложно было найти наглядное изображение тесной дружбы математики и музыки - музыкальную машину из дерева, которая производит звуки при помощи двух тысяч стальных шариков, сконструировали в Швеции. Авторами необычного и до сих пор не существовавшего музыкального инструмента стали участники музыкальной группы Wintergatan.
Стальные шарики небольшого размера - главный элемент в механизме, издающем мелодичные звуки. Внутри машины, на бобине, находится лента, которая задает основную мелодию. Все остальные элементы - это ударные и басы, которым можно задавать различный темп.
На постройку «музыкального механизма будущего», на расчет и постройку, по словам его создателей, ушло больше одного года.
Презентация математика в музыке
Вывод
- В ходе исследования удалось провести параллель между математикой и музыкой, установить между ними прямую связь;
- Были получены результаты о том, как именно связаны цифры и ноты;
- Выяснилось, в каких конкретно областях наблюдается непосредственная связь между гармоничным звучанием мелодии и четкой математической записью.
Полезные ресурсы
Математика и изобразительное искусство Википедия
Популярная механика Математика как искусство: что скрывается за цифрами?
Волошинов А. В. Математика и искусство
Другие документы
Учебный проект Искусство в математике
Основной курс программы Intel Обучение для будущего МФ-16-1 май-июнь 2019