Результаты исследования обучающихся в проекте Сотая доля

Авторы и участники проекта

Грачева Александра

Лепилова Анастасия

Участники группы "Математики"

Тема исследования группы

Применение процентов в математике

Проблемный вопрос (вопрос для исследования)

Как применяются проценты в математике?

Гипотеза исследования

Мы считаем, что процент имеет широкий спектр практической направленности в математике,

а понимание процентов и умение выполнять процентные вычисления и расчеты необходимы каждому человеку.

Цели исследования

1. Ознакомиться с понятием процент;

2. Узнать историю возникновения и развития процентов;

3. Рассмотреть типовые задачи на проценты;

4. Сделать вывод.

Результаты проведённого исследования

Сначала нам нужно определить, что же такое проценты?

Процент - это один из интересных и часто применяемых на практике инструментов. Проценты частично или полностью применяются в любой науке, на любой работе и даже в повседневном общении. Человек, который хорошо разбирающийся в процентах, создаёт впечатление умного и образованного.

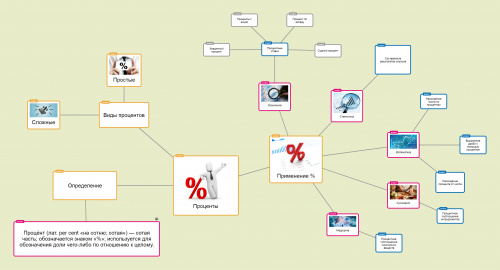
Чтобы более подробно изучить проценты можно воспользоваться Ментальная карта

Далее рассмотрим процесс развития процентов.

Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась ещё в древности у вавилонян, которые пользовались шестидесятеричными дробями. Уже в клинописных табличках вавилонян содержатся задачи на расчет процентов. До нас дошли составленные ими таблицы, которые позволили быстро определять сумму процентных денег. Были известны проценты и в Индии. Индийские математики вычисляли проценты, применяя так называемое тройное правило, т.е. пользуясь пропорцией. Они умели производить более сложные вычисления с применением процентов. Денежные расчёты с процентами были особенно распространены в Древнем Риме. Они называли процентами деньги, которые платил должник заимодавцу за каждую сотню. Римский сенат даже должен был установить максимально допустимый процент, взимаемый с должника, так как некоторые заимодавцы усердствовали в получении процентных денег. От римлян проценты перешли к другим народам.

В средние века в Европе в связи с широким развитием торговли особенно много внимания обращали на умение вычислять проценты. В то время приходилось рассчитывать не только проценты, но и проценты с процентов, т.е. сложные проценты, как называют их в наше время. Отдельные конторы и предприятия для облегчения труда при вычисления процентов разрабатывали свои особые таблицы, которые составляли коммерческий секрет фирмы.

Впервые опубликовал таблицы для расчёта процентов в 1584 г. Симон Стевин - инженер из города Брюгге (Нидерланды). Стевин известен замечательным разнообразием научных открытий, в том числе - особой записи десятичных дробей.

Знак "%" происходит, как полагают, от итальянского слова cento (сто), которое в процентных расчётах часто писалось сокращённо cto. Отсюда путём дальнейшего упрощения в скорописи буквы t в наклонную черту произошёл современный символ для обозначения процента.

Затем рассмотрели несколько типовых задач на проценты и решили их.

Задача 1. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?

Решение:

1) 76 : 100 = 0,76 (кг) 1% от массы человека;

2) 0,76 * 70 = 53,2(кг).

Ответ: масса воды 53,2 кг.

Задача 2. Металлический конструктор состоит из 300 деталей. 12% этих деталей гайки. Сколько гаек в металлическом конструкторе?

Решение:

1) 300 : 100 = 3(детали) 1% всех деталей конструктора;

2) 3 * 12 = 36 (гаек).

Ответ: в конструкторе 36 гаек.

Задача 3. В грушах сладких сортов содержится сахара 15% от их массы. Сколько кг сахара будет содержаться в 6 кг груш?

Решение:

1) 6 : 100 = 0,06 (кг) 1% от шести килограмм;

2) 0,06 * 15 = 0,9 (кг).

Ответ: в шести кг груш будет содержаться 0,9 кг сахара.

Вывод

В процессе исследования, мы пришли к выводу, что история развития процентов - процесс очень длительный и он продолжается и по сей день.

Также мы поняли, что умение выполнять процентные вычисления и расчеты необходимо каждому человеку, так как с процентами мы сталкиваемся в повседневной жизни постоянно. Поэтому считаем, что наша работа найдет практическое применение на уроках математике, как пример решения задач разных видов с практическим содержанием, так и поможет увидеть широту возможных приложений математики, понять её роль в современной жизни.

Цели работы достигнуты.

Полезные ресурсы

Cправочник по математике

Математика в экономике

Учебник по математике 5 класс

"Говорящие проценты"

Методическая разработка по математике "Проценты". Методика решения задач различных типов на проценты

Другие документы

Учебный проект Сотая доля