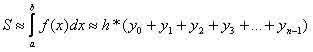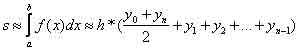Учебный курс Программирование на Delphi. Модуль 16
В качестве примеров программирования на Delphi рассмотрим задачи численного интегрирования и приближенного решения уравнений.
Содержание
Численное интегрирование
Многие инженерные задачи, задачи физики, геометрии и многих других областей человеческой деятельности приводят к необходимости вычислять определенный интеграл вида
![]() ,где f(х) данная функция, непрерывная на отрезке [а; b]. Если функция f(х) задана формулой, то определенный интеграл вычисляется по формуле Ньютона-Лейбница:
,где f(х) данная функция, непрерывная на отрезке [а; b]. Если функция f(х) задана формулой, то определенный интеграл вычисляется по формуле Ньютона-Лейбница:
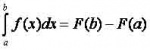
Если же неопределенный интеграл данной функции не известен, или если функция f(х) задана графически или таблицей, то для вычисления определенного интеграла применяют приближенные формулы. Для приближенного вычисления интеграла существует много численных методов, например, метод прямоугольников, метод трапеций, метод Симпсона.
Рассмотрим метод прямоугольников для нахождения интеграла.
Разделим отрезок [а; b] на n равных частей, т.е. на n элементарных отрезков. Длина элементарного отрезка ![]() .
.
Точки деления будут: x0 =a: x1 =a+h: x2 =a+2*h, . . . , xn-1 = a+(n-1)*h; xn =b. Числа у0, у1, у2,. . ., уn являются ординатами точек графика функции, соответствующих абсциссам х0, х1, х2, . . . , хn. Площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из n прямоугольников. Вычисление определенного интеграла сводится к нахождению суммы n элементарных прямоугольников.
Вычисление интеграла с использованием метода трапеций ведется по формуле:
Площадь криволинейной трапеции заменяется площадью многоугольника, составленного из n трапеций.
Решение уравнений
Решение многих практических задач сводятся к решению уравнений f(x)= 0, где функция f(x) определена и непрерывна на некотором интервале. Если функция f(x) представляет собой многочлен, то уравнение f(x) = 0 называется алгебраическим, если же в функцию f(x) входят трансцендентные (тригонометрические, логарифмические, показательные и т.д.) функции, то уравнение f(x) = 0 называется трансцендентным.
Для решения алгебраических уравнений любой степени, трансцендентных уравнений разработаны численные методы. Решение уравнения f(x) = 0 разбивается на 2 этапа:
1. отделение корней, т.е. отыскание достаточно малых областей, в каждой из которых заключен один и только один корень уравнения
2. вычисление выделенного корня с заданной точностью.
Существует множество методов вычисления корней: метод половинного деления, метод проб, метод итераций, метод хорд, метод касательных, комбинированный метод. Рассмотрим метод половинного деления.
Пусть корень уравнения f(x) = 0 на отрезке [a,b] существует, причем функция f(x) непрерывна на этом отрезке и на концах его принимает значения разных знаков, т.е. f(a)*f(b)<0. Разделим отрезок [a,b] пополам точкой c=(a+b)/2. Таким образом, отрезок [a,b] разделен на два отрезка [a,c], [c,b]. Если f(c) = 0, то c и есть корень уравнения, найденный точно. Если f(c) ≠ 0, то выбираем тот отрезок, на концах которого функция f(x) принимает значение разных знаков. Продолжая процесс половинного деления, можно получить сколь угодно малый отрезок, содержащий корень уравнения. Если длина отрезка, меньше заданной точности, то в качестве значения корня берут значение середины данного отрезка.
Пример 1
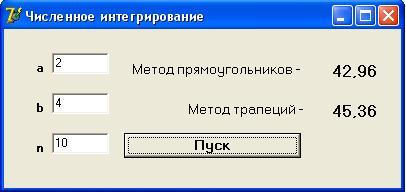
- Условие задачи:
по методу прямоугольников и трапеций:
- Использованные компоненты:
Edit1 - для ввода нижнего предела интегрирования;
Edit2 - для ввода вержнего предела интегрирования;
Edit3 - количество интервалов интегрирования;
Label1 - для вывода значения интеграла по методу прямоугольников;
Label2 - для вывода значения интеграла по методу трапеций;
Button - вывод результата.
- Программный код:
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls;
type
TForm1 = class(TForm)
Edit1: TEdit;
Edit2: TEdit;
Edit3: TEdit;
Label1: TLabel;
Label2: TLabel;
Button1: TButton;
Label4: TLabel;
Label5: TLabel;
Label6: TLabel;
Label3: TLabel;
Label7: TLabel;
procedure Button1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
function f(x:real):real;
begin
f:=2*x*x+4
end;
procedure TForm1.Button1Click(Sender: TObject);
var a,b:real;
n,i:integer;
s,h,Ip,It:real;
begin
a:=StrToFloat(Edit1.Text);
b:=StrToFloat(Edit2.Text);
n:=StrToInt(Edit3.Text);
h:=(b-a)/n;
s:=0;
for i:=0 to n-1 do
s:=s+f(a+i*h);
Ip:=s*h;
label1.Caption:=FloatToStr(Ip);
S:=(f(a)+f(b))/2;
for i:=1 to n-1 do
s:=s+f(a+i*h);
It:=s*h;
label2.caption:=FloatToStr(It);
end;
end.
- Форма с результатом работы программы:
Пример 2
- Условие задачи:
x3-cos(x)=0
найти корни уравнения с помощью метода половинного деления
- Использованные компоненты:
Label1 - для текстового сообщения
Label2 - для вывода значения корня уравнения, найденного с помощью метода половинного деления
Label3 - для вывода значения корня уравнения, найденного графическим способом
Button - кнопка для запуска процедуры поиска корня методом половинного деления
- Программный код:
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls;
type
TForm1 = class(TForm)
Button1: TButton;
Label2: TLabel;
Label1: TLabel;
Label3: TLabel;
procedure FormPaint(Sender: TObject);
procedure FormResize(Sender: TObject);
procedure Button1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
t:real;
implementation
{$R *.dfm}
function f(x:real):real;
begin
f:=x*x*x-COS(x);
end;
procedure gr;
var
x1,x2:real;
y1,y2:real;
x:real;
y:real;
dx:real;
l,b:integer;
w,h:integer;
mx,my:real;
x0,y0:integer;
begin
l:=10;
b:=Form1.clientheight-20;
h:=Form1.clientheight-40;
w:=Form1.clientwidth-40;
x1:=-3; x2:=3; dx:=0.0001;
y1:=f(x1);
y2:=f(x1);
x:=x1;
repeat
y:=f(x);
if y<y1 then y1:=y;
if y>y2 then y2:=y;
x:=x+dx;
until (x>=x2);
my:=h/(abs(y2-y1));
mx:=w/(abs(x2-x1));
x0:=l;
y0:=b-abs(round(y1*my));
with form1.canvas do begin
moveto(l,b); lineto(l,b-h);
moveto(x0,y0); lineto(x0+w,y0);
textout(l+5,b-h,floattostrf(y2,ffgeneral,6,3));
textout(l+5,b,floattostrf(y1,ffgeneral,6,3));
x:=x1;
repeat
y:=f(x);
if abs(y)<0.01 then t:=x;
pixels[x0+round(x*mx),y0-round(y*my)]:=clred;
x:=x+dx;
until (x>=x2);
end;
end;
procedure TForm1.FormPaint(Sender: TObject);
begin
gr;
Label3.Caption:=floattostr(t);
end;
procedure TForm1.FormResize(Sender: TObject);
begin
form1.Canvas.FillRect(rect(0,0,clientwidth,clientheight));
gr;
end;
procedure TForm1.Button1Click(Sender: TObject);
var
a,b,c:real;
y1,y2,e:real;
begin
a:=-3;
b:=3;
e:=0.00001;
repeat
c:=(a+b)/2;
y1:=f(a);
y2:=f(c);
if (y1*y2>0) then a:=c
else b:=c;
until (abs(b-a))<e;
label2.caption:=floattostr(c);
end;
end.
- Форма с результатом работы программы:
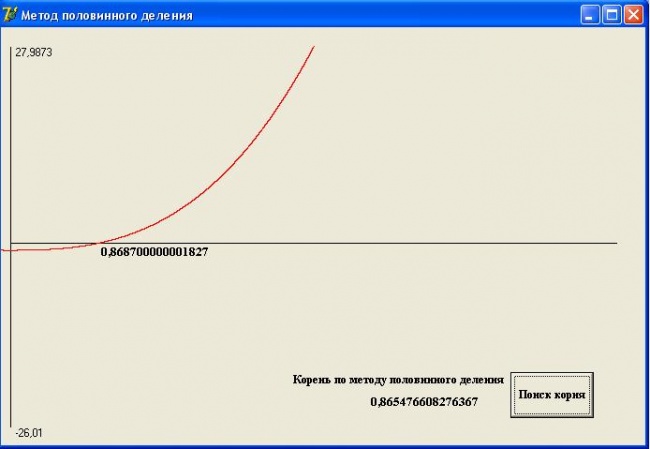
Пример 3
- Условие задачи:
Заданы значения температуры:
Какая температура была в 7 день?
- Использованные компоненты:
- Программный код:
- Форма с результатом работу программы:
Задание
Таблица ...
Найти корни уравнения с точностью e=0.0001
| Номер варианта | Условие | |
|---|---|---|
| F(x)=3^x+x^2-2 | ||
| F(x)=exp(-x^2)-x^2+x | ||
| F(x)=2^(sin(x))-x^2+3 | ||
| F(x)=3^cos(x)-2*log((x-3)^2) | ||
| F(x)=log(4*(x-2)^2)+(x-1)^2-3 | ||
| F(x)=(x+1)*sin(x)+(x-1)^2-3 | ||
| F(x)=exp(sin(x))-(x+1)^2+2 | ||
| F(x)=2*sin(x^2)-(x-1)^2+4 | ||
| F(x)=log(x-2)^2+(x-1)^2/2-5 | ||
| F(x)=log(abs(x-2))+x^2/2-1 | ||
| F(x)=log(x)^2+x-3 | ||
| F(x)=2*x^2/(x^2-1)+log(x-1)-3 | ||
| F(x)=2/x^2-3*log((x-1)^2)+1 | ||
| F(x)=cos(x^2)+(x+1)^2-1 | ||
| F(x)=((x-1)^3)/3-1/x |
Таблица ...
Найти интеграл
| Номер варианта | Условие | a | b | n | |
|---|---|---|---|---|---|
| F(x)=log(x)/(x*sqr(1+log(x))) | 1 | 3.5 | 20 | ||
| F(x)=exp(x)*(1+sin(x))/(1+cos(x)) | 0 | 1.5 | 30 | ||
| F(x)=x/(x^4+3*x^2+2) | 1 | 2 | 20 | ||
| F(x)= 1/(3*sin(x)+2*cos(x))^2 | 0 | 1 | 20 | ||
| F(x)=1/sqr(9+x^2) | 0 | 2 | 30 | ||
| F(x)=1/sqr(x+5) | 1 | 2 | 20 | ||
| F(x)= x*sin(3*x) | 0 | 2 | 25 | ||
| F(x)=x/sqr(x^2-4) | 3 | 5 | 20 | ||
| F(x)=sin(2*x)/(4+cos(2*x)) | 0 | 2 | 30 | ||
| F(x)= 1/(1+exp(2*x)) | 0.5 | 2.5 | 25 | ||
| F(x)= sin(2*x)^2 | 0 | 1.5 | 20 | ||
| F(x)=1/sqr((4-x^2)^3) | 0 | 1 | 30 | ||
| F(x)= sqr(2*x+3) | 1 | 4 | 30 | ||
| F(x)=x^2/(2*x+1)^2 | 1 | 3 | 20 | ||
| F(x)=1/sqr(x+2) | 0 | 2.5 | 25 |
Литература
- Архангельский. Программирование на Delphi 6. – М: БИНОМ, 2002
- Бобровский С. Delphi 7. Учебный курс. – СПб: Питер, 2003
- Культин Н. Основы программирования в Delphi 7. СПб: БХВ-Петербург, 2005.