Учебный курс Программирование на Delphi. Модуль 7: различия между версиями
(→Задание) |
(→Задание) |
||
| Строка 167: | Строка 167: | ||
Вычисления продолжать пока [[Изображение:Задание14-1.JPG]]не станет меньше заданной точности Е. | Вычисления продолжать пока [[Изображение:Задание14-1.JPG]]не станет меньше заданной точности Е. | ||
|} | |} | ||
| − | + | <center>'''Таблица 14'''</center> | |
| − | + | ||
| − | + | ||
| + | {| border=2 | ||
| + | |- | ||
| + | |<center>'''№ варианта'''</center> | ||
| + | |<center>'''Условие'''</center> | ||
| + | |- | ||
| + | |<center>1</center> | ||
| + | |[[Изображение:Формула1.JPG]] | ||
| + | |- | ||
| + | |<center>2</center> | ||
| + | |[[Изображение:Формула2.JPG]] | ||
| + | |- | ||
| + | |<center>3</center> | ||
| + | |[[Изображение:Формула3.JPG]] | ||
| + | |||
| + | |- | ||
| + | |<center>4</center> | ||
| + | |[[Изображение:Формула4.JPG]] | ||
| + | |- | ||
| + | |<center>5</center> | ||
| + | |[[Изображение:Формула5.JPG]] | ||
| + | |- | ||
| + | |<center>6</center> | ||
| + | |[[Изображение:Формула6.JPG]] | ||
| + | |- | ||
| + | |<center>7</center> | ||
| + | |[[Изображение:Формула7.JPG]] | ||
| + | |- | ||
| + | |<center>8</center> | ||
| + | |[[Изображение:Формула8.JPG]] | ||
| + | |- | ||
| + | |<center>9</center> | ||
| + | |[[Изображение:Формула9.JPG]] | ||
| + | |- | ||
| + | |<center>10</center> | ||
| + | |[[Изображение:Формула10.JPG]] | ||
| + | |- | ||
| + | |<center>11</center> | ||
| + | |[[Изображение:Формула11.JPG]] | ||
| + | |- | ||
| + | |<center>12</center> | ||
| + | |[[Изображение:Формула12.JPG]] | ||
| + | |- | ||
| + | |<center>13</center> | ||
| + | |[[Изображение:Формула13.JPG]] | ||
| + | |- | ||
| + | |<center>14</center> | ||
| + | |[[Изображение:Формула14.JPG]] | ||
| + | |} | ||
==Литература== | ==Литература== | ||
Версия 09:40, 11 апреля 2008
Для программирования циклов с условием в Delphi существуют оператор цикла с предусловием WHILE и оператор цикла с постусловием REPEAT.
Формат операторов:
while условие do оператор;
repeat операторы until условие;
условие – логическое выражение.
В операторе while сначала вычисляется логическое выражение и если оно истинно, то выполняется оператор. После этого управление возвращается в начало цикла на вычисление логического выражения. Если условие ложно, оператор завершает работу и управление передаётся на следующий оператор.
В операторе repeat сначала выполняются операторы, и только потом вычисляется логическое выражение. Если оно ложно, то управление возвращается в начало цикла, повторяется выполнение операторов тела цикла. Если условие истинно – то выход из цикла.
Содержание
Пример 1.
- Условие
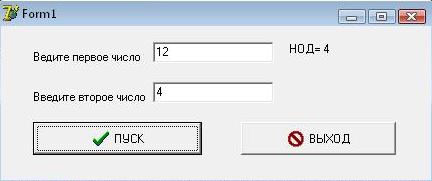
Алгоритм Евклида для подсчета НОД (наибольшего общего делителя) двух натуральных чисел.
- Использованные компоненты
- Программный код
var a,b,x,y,z:integer;
procedure TForm1.BitBtn2Click(Sender: TObject); begin close; end;
procedure TForm1.BitBtn1Click(Sender: TObject);
begin
a:=strtoint(edit1.Text); b:=strtoint(edit2.Text);
x:=a; y:=b;
while (x<>y) do
if x>y then x:=x-y
else y:=y-x;
z:=x;
label3.Caption:='НОД= '+inttostr(z); end; end.
- Форма с результатом работы программы
Пример 2.
- Условие
- Использованные компоненты
- Программный код
var n:integer;
s,z,e:real;
procedure TForm1.BitBtn2Click(Sender: TObject); begin close; end;
procedure TForm1.BitBtn1Click(Sender: TObject); begin e:=strtofloat(edit1.Text); n:=1; z:=1/6; s:=0;
while abs(z)>=e do
begin
s:=s+z;
n:=n+1;
z:=n/((n+1)*(n+2));
end;
label2.Caption:='Сумма= '+floattostr(s); end;
end.
- Форма с результатом работы программы
Пример 3.
- Условие
- Использованные компоненты
- Программный код
var x1,x2,d,e,m:real; procedure TForm1.BitBtn2Click(Sender: TObject); begin close; end;
procedure TForm1.BitBtn1Click(Sender: TObject); begin m:=strtofloat(edit1.Text); e:=strtofloat(edit2.Text); x1:=m;
repeat x2:=2/3*x1+m/3/sqr(x1); d:=abs(x1-x2); x1:=x2; until d<=e;
label3.Caption:='Корень= '+floattostr(x2); end;
end.
- Форма с результатом работы программы
Задание
| Вычислить квадратный корень из заданного числа x с точностью Е по итерационному методу Ньютона по формуле: | |
| Для выражения exp(k)/k определить наименьшее k, при котором значение выражения становится больше заданного числа n. | |
| Найти наибольшую степень двойки, не превышающую заданного числа n | |
| Ввести и просуммировать любое количество целочисленных значений. Если введено значение 999, то вывести результат суммирования. | |
| Найти наименьшее общее кратное двух чисел. | |
| Найти наибольшую степень 3, не превышающую заданного числа m. | |
| Для выражения Файл:Таблица9 Задание7.JPG определить наименьшее k, при котором значение выражения становится больше заданного числа m. | |
| Кощей Бессмертный зарыл клад на глубину 1 м. Этого ему показалось не достаточно, он отрыл клад, углубил колодец до 2 м и снова зарыл. Этого ему опять показалось мало, он отрыл клад, углубил колодец до 3 м и зарыл. Затем он проделал тоже, углубив колодец до 4 м, потом до 5 м, 6 м и т.д. Известно, что колодец глубиной n метров Кощей вырывает за n2 дней. Известно также, что на 1001-й день Кощей умер от непосильной работы. На какой глубине остался клад? (Временем, необходимым для закапывания клада, пренебречь). | |
| Два параллельных зеркала А и В обращены друг к другу. При падении луча на зеркало А он ослабляется на Т[%], а при его падении на зеркало В - на Р[%]. Определить, после скольких отражений луч, попеременно отражаясь то от зеркала А, то от зеркала В, ослабеет более чем в 50 раз. Первоначально он попадает на зеркало А. | |
| В водохранилище каждые сутки поступает Т [м3] воды, а расходуется R [ м3] на орошение полей и испарение, к тому же ежесуточно теряется А(1-exp(-V)) [м3] воды на просачивание в почву, где А - коэффициент , V - объем воды в водохранилище. Определить, за сколько дней объем воды в водохранилище уменьшится на Р [%] заданного первоначального объема V0. Принять А = 100. | |
| Найти число в последовательности Фибоначчи большее заданного числа m и его порядковый номер. Члены ряда Фибоначчи вычисляются по формуле:
F(1) = F(2) = 1 F(k) = F(k-1) + F(k-2), k > 2 | |
| На железнодорожном пути находится n разрозненных вагонов. К ним движется вагон с кинетической энергией W, он сцепляется с ближайшим вагоном, затем вместе с ним движется дальше, сцепляясь с очередным вагоном, и т.д. При каждой сцепке расходуется 20% имеющейся кинетической энергии, еще Р[ Дж ] затрачивается на то, чтобы стронуть с места неподвижный вагон и, если энергия не истрачена полностью, движение продолжается. Определить, сколько вагонов окажутся сцепленными. | |
| Вычислить значения функции:
Файл:Задание13.JPG
| |
| Извлечь корень степени m из числа x, воспользовавшись итерационной формулой:
Файл:Задание14.JPG
|
| Файл:Формула1.JPG | |
| Файл:Формула2.JPG | |
| Файл:Формула3.JPG | |
| Файл:Формула4.JPG | |
| Файл:Формула5.JPG | |
| Файл:Формула6.JPG | |
| Файл:Формула9.JPG | |
| Файл:Формула10.JPG | |
| Файл:Формула11.JPG | |
| Файл:Формула12.JPG | |
| Файл:Формула13.JPG | |
| Файл:Формула14.JPG |
Литература
- Архангельский. Программирование на Delphi 6. – М: БИНОМ, 2002
- Бобровский С. Delphi 7. Учебный курс. – СПб: Питер, 2003
- Культин Н. Основы программирования в Delphi 7. СПб: БХВ-Петербург, 2005.