Учебный курс Программирование на Delphi. Модуль 3: различия между версиями
(→Задание) |
|||
| (не показано 7 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
<center>'''Программирование на Delphi линейных алгоритмов'''</center> | <center>'''Программирование на Delphi линейных алгоритмов'''</center> | ||
| Строка 30: | Строка 29: | ||
Object Pascal поддерживает и наиболее универсальный целый тип - Integer, который эквивалентен Longint. | Object Pascal поддерживает и наиболее универсальный целый тип - Integer, который эквивалентен Longint. | ||
| − | + | ''Вещественный тип'' | |
Язык Delphi поддерживает шесть вещественных типов. Типы различаются между собой диапазоном допустимых значений, количеством значащих цифр и количеством байтов, необходимых для хранения данных в памяти компьютера (табл. 2). | Язык Delphi поддерживает шесть вещественных типов. Типы различаются между собой диапазоном допустимых значений, количеством значащих цифр и количеством байтов, необходимых для хранения данных в памяти компьютера (табл. 2). | ||
| Строка 74: | Строка 73: | ||
Логическая величина может принимать одно из двух значений True (истина) или False (ложь). В языке Delphi логические величины относят к типу Boolean. | Логическая величина может принимать одно из двух значений True (истина) или False (ложь). В языке Delphi логические величины относят к типу Boolean. | ||
| + | |||
== Линейный алгоритм == | == Линейный алгоритм == | ||
Алгоритм решения любой задачи на ЭВМ можно получить, используя и комбинируя только три структуры: последовательную, структуру ветвления и структуру цикла. | Алгоритм решения любой задачи на ЭВМ можно получить, используя и комбинируя только три структуры: последовательную, структуру ветвления и структуру цикла. | ||
| Строка 170: | Строка 170: | ||
*Условие. Найти сопротивление цепи из двух последовательно соединенных проводников. | *Условие. Найти сопротивление цепи из двух последовательно соединенных проводников. | ||
*Использованные компоненты | *Использованные компоненты | ||
| + | Edit1 – ввод числа R1; | ||
| − | Edit1 – ввод | + | Edit1 – ввод числа R2; |
| − | |||
| − | |||
| − | + | Label1 - вывод результирующего сопротивления; | |
| − | + | Button1 - запуск программы; | |
| + | Button2 - выход из программы; | ||
| + | *'''Программный код''' | ||
| + | |||
| + | unit Unit1; | ||
| + | |||
| + | interface | ||
| + | |||
| + | uses | ||
| + | Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, | ||
| + | Dialogs, StdCtrls, Buttons; | ||
| + | |||
| + | type | ||
| + | TForm1 = class(TForm) | ||
| + | Edit1: TEdit; | ||
| + | Edit2: TEdit; | ||
| + | Label1: TLabel; | ||
| + | Label2: TLabel; | ||
| + | Label3: TLabel; | ||
| + | BitBtn1: TBitBtn; | ||
| + | BitBtn2: TBitBtn; | ||
| + | procedure BitBtn2Click(Sender: TObject); | ||
| + | procedure BitBtn1Click(Sender: TObject); | ||
| + | private | ||
| + | { Private declarations } | ||
| + | public | ||
| + | { Public declarations } | ||
| + | end; | ||
| + | |||
| + | var | ||
| + | Form1: TForm1; | ||
| + | |||
| + | implementation | ||
| + | {$R *.dfm} | ||
| + | procedure TForm1.BitBtn2Click(Sender: TObject); | ||
| + | begin | ||
| + | Close; | ||
| + | end; | ||
| + | var r1,r2,r:integer; | ||
| + | procedure TForm1.BitBtn1Click(Sender: TObject); | ||
| + | begin | ||
| + | r1:=strtoint(edit1.Text); | ||
| + | r2:=strtoint(edit2.Text); | ||
| + | r:=r1+r2; | ||
| + | label3.Caption:='Сопротивление 1-го проводника= '+inttostr(r1)+ | ||
| + | #13+'Сопротивление 2-го проводника= '+inttostr(r2)+#13+'Сопротивление цепи= '+inttostr(r) | ||
| + | end; | ||
| + | end. | ||
| + | |||
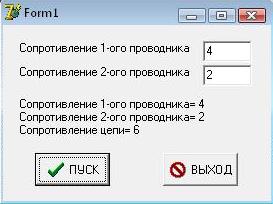
| + | *'''Форма с результатом работы программы''' | ||
| + | |||
| + | [[Изображение:-1-1.JPG]] | ||
==Задание== | ==Задание== | ||
| − | Таблица | + | Таблица 2 |
{| border=1 | {| border=1 | ||
!Номер варианта||Условие||Исходные данные|| | !Номер варианта||Условие||Исходные данные|| | ||
|- | |- | ||
| − | + | |<center>1</center>||Определить расстояние d между двумя точками на плоскости||х1, у1, x2, y2|<center>x1,y1,x2,y2</center> | |
|- | |- | ||
| − | + | |<center>2</center>||Заданы 4 числа. Вычислить среднее арифметическое и среднее геометрическое их модулей||<center>a, в, c, d</center> | |
|- | |- | ||
| − | + | |<center>3</center>|| Найти радиус окружности, описанной вокруг треугольника по формуле: | |
| − | + | R=(a*b*c)/(4*SQRT(p*(p-a)*(p-b)*(p-c))), | |
где р - полупериметр | где р - полупериметр | ||
| − | ||а, в, с | + | ||<center>а, в, с</center> |
|- | |- | ||
| − | + | |<center>4</center>||Найти радиус круга, вписанного в треугольник со сторонами а, в, с по формуле: | |
| − | + | r=(SQRT(p*(p-a)*(p-b)*(p-c)))/p, | |
где р - полупериметр | где р - полупериметр | ||
| − | ||а, в, с | + | ||<center>а, в, с</center> |
|- | |- | ||
| − | + | |<center>5</center>||Определить площадь треугольника по трем углам и высоте: | |
| − | ||A, B, C, h | + | ||<center>A, B, C, h</center> |
|- | |- | ||
| − | + | |<center>6</center>||Определить площадь треугольника по заданной стороне и углам: | |
| − | + | S=(SQR(h)*sin(A))/(2*sin(B)*sin(C)), | |
| − | |||
| − | |||
где р - полупериметр | где р - полупериметр | ||
| − | ||A, B, C, a | + | ||<center>A, B, C, a</center> |
|- | |- | ||
| − | + | |<center>7</center>||Вычислить сопротивление цепи: | |
| − | ||R1, R2, R3 | + | ||<center>R1, R2, R3</center> |
|- | |- | ||
| − | + | |<center>8</center>||Вычислить сопротивление цепи: | |
где р - полупериметр | где р - полупериметр | ||
| − | ||R1, R2, R3 | + | ||<center>R1, R2, R3</center> |
|- | |- | ||
| − | + | |<center>9</center>||По двум сторонам и углу между ними в треугольнике АВС найти два остальных угла и третью сторону. | |
| − | + | SQR(C)=SQR(A)+SQR(B)-2*A*B*cos(x) | |
| − | ||A, B, | + | ||<center>A, B, x</center> |
|- | |- | ||
| − | + | |<center>11</center>||Найти площадь ромба по стороне и острому углу: | |
| − | + | S=SQR(a)*sin(x), | |
| + | где а - сторона , x-угол | ||
| − | ||а, | + | ||<center>а, x</center> |
|- | |- | ||
| − | + | |<center>12</center>|| В арифметической прогрессии известны 1-й член и разность. Найти 30-й член этой прогрессии и сумму первых 40 членовгде р - полупериметр | |
| − | ||а1, d | + | ||<center>а1, d</center> |
|- | |- | ||
| − | + | |<center>13</center>||Найти координаты центра отрезка, заданного координатами его концов. | |
| − | ||x1, y1, x2, y2 | + | ||<center>x1, y1, x2, y2</center> |
|- | |- | ||
| − | + | |<center>14</center>||Найти сумму всех натуральных чисел от 1 до m, используя формулу суммы членов арифметической прогрессии.||<center>m</center> | |
|} | |} | ||
| − | Таблица | + | Таблица 3 |
{| border=1 | {| border=1 | ||
!Номер варианта||Условие||Исходные данные|| | !Номер варианта||Условие||Исходные данные|| | ||
|- | |- | ||
| − | + | |<center>1</center>||Найти произведение цифр заданного четырехзначного числа||<center>n</center> | |
|- | |- | ||
| − | + | |<center>2</center>||Найти площадь кольца с внутренним радиусом r и внешним радиусом R (r< R)||<center>r, R</center> | |
|- | |- | ||
| − | + | |<center>3</center>||Не используя никаких функций и никаких операций, кроме умножения, получить a8 за три операции.||<center>a</center> | |
|} | |} | ||
| − | Таблица | + | Таблица 4 |
{| border=1 | {| border=1 | ||
!Номер варианта||Условие||Исходные данные|| | !Номер варианта||Условие||Исходные данные|| | ||
|- | |- | ||
| − | |<center>1</center>|| Треугольник со сторонами a, b, c является равнобедренным ||a, b, c | + | |<center>1</center>|| Треугольник со сторонами a, b, c является равнобедренным ||<center>a, b, c</center> |
|- | |- | ||
| − | |<center>2</center>||Данное четырехзначное число читается одинаково слева направо и справа налево|| | + | |<center>2</center>||Данное четырехзначное число читается одинаково слева направо и справа налево|||<center>m</center> |
|- | |- | ||
| − | |<center>3</center>||Данное целое число является четным| | + | |<center>3</center>||Данное целое число является четным||<center>n</center> |
|- | |- | ||
| − | |<center>4</center>||Сумма двух первых цифр заданного четырехзначного числа равна сумме двух его последних цифр| | + | |<center>4</center>||Сумма двух первых цифр заданного четырехзначного числа равна сумме двух его последних цифр||<center>n</center> |
|- | |- | ||
| − | |<center>5</center>||Треугольник со сторонами a, b, c является равносторонним||a, b, c | + | |<center>5</center>||Треугольник со сторонами a, b, c является равносторонним||<center>a, b, c</center> |
|- | |- | ||
| − | |<center>6</center>||Данное целое число a кратно числу b||a, b | + | |<center>6</center>||Данное целое число a кратно числу b||<center>a, b</center> |
|- | |- | ||
| − | |<center>7</center>||Число с является средним арифметическим чисел a и b||a, b | + | |<center>7</center>||Число с является средним арифметическим чисел a и b||<center>a, b</center> |
|- | |- | ||
| − | |<center>8</center>||Сумма цифр данного четырехзначного числа является четным числом| | + | |<center>8</center>||Сумма цифр данного четырехзначного числа является четным числом||<center>m</center> |
|- | |- | ||
| − | |<center>9</center>||Числа x и y являются координатами точки, лежащей в третьей координатной четверти||x, y | + | |<center>9</center>||Числа x и y являются координатами точки, лежащей в третьей координатной четверти||<center>x, y</center> |
|- | |- | ||
| − | |<center>10</center>||Произведение чисел a и b кратно числу c||a, b, c | + | |<center>10</center>||Произведение чисел a и b кратно числу c||<center>a, b, c</center> |
|- | |- | ||
| − | |<center>11</center>||Данная тройка натуральных чисел a, b, c является тройкой Пифагора, т.е. c2 = a2 + b2||a, b, c | + | |<center>11</center>||Данная тройка натуральных чисел a, b, c является тройкой Пифагора, т.е. c2 = a2 + b2||<center>a, b, c</center> |
|- | |- | ||
| − | |<center>12</center>||Сумма цифр данного трехзначного числа является нечетным числом| | + | |<center>12</center>||Сумма цифр данного трехзначного числа является нечетным числом||<center>m</center> |
|- | |- | ||
| − | |<center>13</center>||Сумма двух натуральных чисел кратна трем||a, b | + | |<center>13</center>||Сумма двух натуральных чисел кратна трем||<center>a, b</center> |
|- | |- | ||
| − | |<center>14</center>||Периметр треугольника со сторонами a, b, c больше числа d||a, b, c, d | + | |<center>14</center>||Периметр треугольника со сторонами a, b, c больше числа d||<center>a, b, c, d</center> |
|} | |} | ||
Текущая версия на 07:19, 19 апреля 2008
Содержание
Типы данных Delphi
Целый тип
Язык Delphi поддерживает семь целых типов данных, описание которых приведено в табл. 1. Таблица 1. Целые типы
| Тип | Диапазон | Формат | |
|---|---|---|---|
| Shortint | -128 - 127 | 8 битов | |
| Smallint | -32768 - 32767 | 16 битов | |
| Longint | -2147483648 - 2147483647 | 32 бита | |
| Int64 | -263 -2 63-1 | 64 бита | |
| Byte | 0 - 255 | 8 битов | |
| Word | 0 - 65535 | 16 битов | |
| Longword | 0 - 4294967295 | 32 бита |
Object Pascal поддерживает и наиболее универсальный целый тип - Integer, который эквивалентен Longint.
Вещественный тип
Язык Delphi поддерживает шесть вещественных типов. Типы различаются между собой диапазоном допустимых значений, количеством значащих цифр и количеством байтов, необходимых для хранения данных в памяти компьютера (табл. 2).
Таблица 2. Вещественные (дробные) типы
| Тип | Диапазон | Значащих цифр | Байтов | |
|---|---|---|---|---|
| Real48 | 2.9 x 10 -39 - 1.7 x 1038 | 11 – 12 | 6 | |
| Single | 1.5 x 10 -45 - 3.4 x 1038 | 7 – 8 | 4 | |
| Double | 5.0 x 10 -324 - 1.7 x 10308 | 15 – 16 | 8 | |
| Extended | 3.6 x 10 -4951 - 1.1 x 104932 | 19 – 20 | 10 | |
| Comp | -2 63 +1 - 2 63 -1 | 19 – 20 | 8 | |
| Currency | -9223372036854775808 - 9223372036854775807 | 19 –20 | 8 |
Язык Delphi поддерживает и наиболее универсальный вещественный тип - Real, который эквивалентен Double.
Символьный тип
Язык Delphi поддерживает два символьных типа: Ansichar и Widechar:
- тип Ansichar — это символы в кодировке ANSI, которым соответствуют числа в диапазоне от 0 до 255;
- тип widechar — это символы в кодировке Unicode, им соответствуют числа от 0 до 65535.
Object Pascal поддерживает и наиболее универсальный символьный тип - Char, который эквивалентен Ansichar.
Строковый тип
Язык Delphi поддерживает три строковых типа: shortstring, Longstring и WideString:
- тип shortstring представляет собой статически размещаемые в памяти компьютера строки длиной от 0 до 255 символов;
- тип Longstring представляет собой динамически размещаемые в памяти строки, длина которых ограничена только объемом свободной памяти;
- тип WideString представляет собой динамически размещаемые в памяти строки, длина которых ограничена только объемом свободной памяти. Каждый символ строки типа WideString является Unicode-символом.
В языке Delphi для обозначения строкового типа допускается использование идентификатора string. Тип string эквивалентен типу shortstring.
Логический тип
Логическая величина может принимать одно из двух значений True (истина) или False (ложь). В языке Delphi логические величины относят к типу Boolean.
Линейный алгоритм
Алгоритм решения любой задачи на ЭВМ можно получить, используя и комбинируя только три структуры: последовательную, структуру ветвления и структуру цикла.
Последовательная структура, которую называют также линейным процессом, состоит в последовательном выполнении одного оператора (блоков операторов) за другим без каких – либо переходов.
При написании сложных программ их алгоритм сначала всегда представляют линейным: ввод данных – обработка их – вывод. Затем детализируется каждый блок программы, алгоритм и программа усложняются. При структурном программировании работа (и программа) каждого блока не зависит от других блоков. Нужно только знать входные и выходные данные. Такой принцип позволяет писать отдельные блоки разным программистам (т.е. сложную программу может писать коллектив программистов), уменьшает количество ошибок в программах, ускоряет процесс их отладки.
Инструкция присваивания
Инструкция присваивания является основной вычислительной инструкцией. Если в программе надо выполнить вычисление, то нужно использовать инструкцию присваивания. В результате выполнения инструкции присваивания значение переменной меняется, ей присваивается значение. Общий вид инструкции присваивания: Имя переменной : = Выражение; Выражение состоит из операндов и операторов. Операторы находятся между операндами и обозначают действия, которые выполняются над операндами. В качестве операндов выражения можно использовать: переменную, константу, функцию или другое выражение. Основные алгебраические операторы приведены в табл. 3.
Таблица 3. Алгебраические операторы
| Оператор | Действие | |
|---|---|---|
| - | Вычитание | |
| * | Умножение | |
| / | Деление | |
| DIV | Деление нацело | |
| MOD | Вычисление остатка от деления |
Стандартные функции
Математические функции указаны в таблице 4.
Таблица 4. Математические функции
| Функция | Значение | |
|---|---|---|
| Abs(x) | Модуль x | |
| Sqrt(x) | Квадратный корень из x | |
| Sqr(x) | Квадрат x | |
| Sin(x) | Синус x | |
| Cos(x) | Косинус x | |
| Arctan(x) | Арктангенс x | |
| Exp(x) | Экспонента x | |
| Ln(x) | Натуральный логарифм x | |
| Random(x) | Случайное целое число в диапазоне от 0 до x-1 |
Функции преобразования
Функции преобразования (табл. 5) наиболее часто используются в инструкциях, обеспечивающих ввод и вывод информации. Таблица 5. Функции преобразования
| Функция | Значение функции | |
|---|---|---|
| Chr(x) | Символ, код которого равен x | |
| IntToStr(x) | Строка, являющаяся изображением целого x | |
| FloatToStr(x) | Строка, являющаяся изображением вещественного x | |
| FloatToStrF(x, f, k,m) | Строка, являющаяся изображением вещественного x. f — формат; k — общее количество цифр; m — количество цифр после десятичной точки | |
| StrToInt(s) | Целое, изображением которого является строка s | |
| StrToFloat (s) | Целое, изображением которого является строка s | |
| Round(x) | Целое, полученное путем округления x | |
| Trunc(x) | Целое, полученное путем отбрасывания дробной части x | |
| Frac(x) | Дробное, представляющее собой дробную часть вещественного x | |
| Int(x) | Дробное, представляющее собой целую часть вещественного x |
Пример
- Условие. Найти сопротивление цепи из двух последовательно соединенных проводников.
- Использованные компоненты
Edit1 – ввод числа R1;
Edit1 – ввод числа R2;
Label1 - вывод результирующего сопротивления;
Button1 - запуск программы;
Button2 - выход из программы;
- Программный код
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Buttons;
type
TForm1 = class(TForm)
Edit1: TEdit;
Edit2: TEdit;
Label1: TLabel;
Label2: TLabel;
Label3: TLabel;
BitBtn1: TBitBtn;
BitBtn2: TBitBtn;
procedure BitBtn2Click(Sender: TObject);
procedure BitBtn1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
procedure TForm1.BitBtn2Click(Sender: TObject);
begin
Close;
end;
var r1,r2,r:integer;
procedure TForm1.BitBtn1Click(Sender: TObject);
begin
r1:=strtoint(edit1.Text);
r2:=strtoint(edit2.Text);
r:=r1+r2;
label3.Caption:='Сопротивление 1-го проводника= '+inttostr(r1)+
#13+'Сопротивление 2-го проводника= '+inttostr(r2)+#13+'Сопротивление цепи= '+inttostr(r)
end;
end.
- Форма с результатом работы программы
Задание
Таблица 2
| Номер варианта | Условие | Исходные данные | |
|---|---|---|---|
| Определить расстояние d между двумя точками на плоскости | |||
| Заданы 4 числа. Вычислить среднее арифметическое и среднее геометрическое их модулей | |||
Найти радиус окружности, описанной вокруг треугольника по формуле:
R=(a*b*c)/(4*SQRT(p*(p-a)*(p-b)*(p-c))), где р - полупериметр |
|||
Найти радиус круга, вписанного в треугольник со сторонами а, в, с по формуле:
r=(SQRT(p*(p-a)*(p-b)*(p-c)))/p, где р - полупериметр |
|||
| Определить площадь треугольника по трем углам и высоте: | |||
Определить площадь треугольника по заданной стороне и углам:
S=(SQR(h)*sin(A))/(2*sin(B)*sin(C)), где р - полупериметр |
|||
| Вычислить сопротивление цепи: | |||
| Вычислить сопротивление цепи:
где р - полупериметр |
|||
По двум сторонам и углу между ними в треугольнике АВС найти два остальных угла и третью сторону.
SQR(C)=SQR(A)+SQR(B)-2*A*B*cos(x) |
|||
Найти площадь ромба по стороне и острому углу:
S=SQR(a)*sin(x), где а - сторона , x-угол |
|||
| В арифметической прогрессии известны 1-й член и разность. Найти 30-й член этой прогрессии и сумму первых 40 членовгде р - полупериметр | |||
| Найти координаты центра отрезка, заданного координатами его концов. | |||
| Найти сумму всех натуральных чисел от 1 до m, используя формулу суммы членов арифметической прогрессии. |
Таблица 3
| Номер варианта | Условие | Исходные данные | |
|---|---|---|---|
| Найти произведение цифр заданного четырехзначного числа | |||
| Найти площадь кольца с внутренним радиусом r и внешним радиусом R (r< R) | |||
| Не используя никаких функций и никаких операций, кроме умножения, получить a8 за три операции. |
Таблица 4
| Номер варианта | Условие | Исходные данные | |
|---|---|---|---|
| Треугольник со сторонами a, b, c является равнобедренным | |||
| Данное четырехзначное число читается одинаково слева направо и справа налево | |||
| Данное целое число является четным | |||
| Сумма двух первых цифр заданного четырехзначного числа равна сумме двух его последних цифр | |||
| Треугольник со сторонами a, b, c является равносторонним | |||
| Данное целое число a кратно числу b | |||
| Число с является средним арифметическим чисел a и b | |||
| Сумма цифр данного четырехзначного числа является четным числом | |||
| Числа x и y являются координатами точки, лежащей в третьей координатной четверти | |||
| Произведение чисел a и b кратно числу c | |||
| Данная тройка натуральных чисел a, b, c является тройкой Пифагора, т.е. c2 = a2 + b2 | |||
| Сумма цифр данного трехзначного числа является нечетным числом | |||
| Сумма двух натуральных чисел кратна трем | |||
| Периметр треугольника со сторонами a, b, c больше числа d |
Литература
- Архангельский. Программирование на Delphi 6. – М: БИНОМ, 2002
- Бобровский С. Delphi 7. Учебный курс. – СПб: Питер, 2003
- Культин Н. Основы программирования в Delphi 7. СПб: БХВ-Петербург, 2005.