Учебный курс Программирование на Delphi. Модуль 4: различия между версиями
Материал из Wiki Mininuniver
Перейти к навигацииПерейти к поиску (→Задание) |
|||
| (не показано 14 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''Программирование на Delphi разветвляющихся алгоритмов''' | + | <center>'''Программирование на Delphi разветвляющихся алгоритмов'''</center> |
| − | == | + | ==Оператор If== |
| − | + | Алгоритм называется разветвляющимся, если он содержит несколько ветвей, отличающихся друг от друга содержанием вычислений. Выход вычислительного процесса на ту или иную ветвь алгоритма определяется исходными данными задачи. | |
| − | |||
| − | + | ==Пример 1== | |
| − | + | *'''Условие задачи''' | |
| − | |||
| − | * | ||
| − | * | + | Найти максимальную из двух величин а и в |
| + | *'''Использованные компоненты''' | ||
| + | Edit1 – для ввода первого числа | ||
| − | + | Edit2 – для ввода второго числа | |
| − | + | Label1 - для вывода описания | |
| + | Label2 - для вывода описания | ||
| − | ==Литература== | + | Label3 - для вывода результирующего сопротивления |
| + | |||
| + | BitBtn1 - для запуска решения | ||
| + | |||
| + | BitBtn2 - для выхода из формы | ||
| + | |||
| + | *'''Программный код''' | ||
| + | unit Unit1; | ||
| + | <br> | ||
| + | interface | ||
| + | |||
| + | uses | ||
| + | Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, | ||
| + | Dialogs, StdCtrls, Buttons; | ||
| + | <br> | ||
| + | type | ||
| + | TForm1 = class(TForm) | ||
| + | Label1: TLabel; | ||
| + | Label2: TLabel; | ||
| + | Edit1: TEdit; | ||
| + | Edit2: TEdit; | ||
| + | Label3: TLabel; | ||
| + | BitBtn1: TBitBtn; | ||
| + | BitBtn2: TBitBtn; | ||
| + | procedure BitBtn2Click(Sender: TObject); | ||
| + | procedure BitBtn1Click(Sender: TObject); | ||
| + | private | ||
| + | { Private declarations } | ||
| + | public | ||
| + | { Public declarations } | ||
| + | end; | ||
| + | <br> | ||
| + | var | ||
| + | Form1: TForm1; | ||
| + | <br> | ||
| + | implementation | ||
| + | <br> | ||
| + | {$R *.dfm} | ||
| + | var a,b,m:real; | ||
| + | procedure TForm1.BitBtn2Click(Sender: TObject); | ||
| + | begin | ||
| + | Close; | ||
| + | end; | ||
| + | <br> | ||
| + | procedure TForm1.BitBtn1Click(Sender: TObject); | ||
| + | begin | ||
| + | a:=strtofloat(edit1.Text); | ||
| + | b:=strtofloat(edit2.Text); | ||
| + | if a>=b then m:=a else m:=b; | ||
| + | <br> | ||
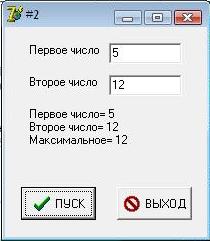
| + | label3.caption:='Первое число= '+floattostr(a)+#13+'Второе число= ' | ||
| + | +floattostr(b)+#13+'Максимальное= '+floattostr(m); | ||
| + | end; | ||
| + | <br> | ||
| + | end. | ||
| + | |||
| + | *'''Форма с результатом работы программы''' | ||
| + | |||
| + | |||
| + | [[Изображение:-2-1.JPG|center]] | ||
| + | |||
| + | ==Задание == | ||
| + | |||
| + | Таблица 5 | ||
| + | {| border=1 | ||
| + | !Номер варианта||Условие||Исходные данные|| | ||
| + | |- | ||
| + | |<center>1</center>||Три точки на плоскости заданы своими координатами.Выяснить какие из них находятся на максимальном расстоянии друг от друга||<center>x1,y1,x2,y2,x3,y3</center> | ||
| + | |- | ||
| + | |||
| + | |<center>2</center>||Вычислить: max^3(a,b,c)+min^2(a,b,c)||<center>a,b,c</center> | ||
| + | |- | ||
| + | |<center>3</center>||Заданы три величины а, b, c. Определить максимальное и минимальное значение из их среднего геометрического, среднего арифметического и суммы экспонент exp(a) + exp(b) + exp(c)||<center>a,b,c</center> | ||
| + | |- | ||
| + | |<center>4</center>||Определить в какой четверти координатной плоскости находится точка с координатами х,у||<center>x,y</center> | ||
| + | |- | ||
| + | |<center>5</center>||m=max(x,y,z) \ min ^ 2(a,b,c)||<center>x,y,z</center> | ||
| + | |- | ||
| + | |<center>6</center>||Z=min(0,x) - min(0,y) \ max ^ 2(y,x)||<center>x,y</center> | ||
| + | |- | ||
| + | |<center>7</center>||r=max(min(x,y),z)/3||<center>x,y,z</center> | ||
| + | |- | ||
| + | |<center>8</center>||v=max(min(x-y,y-x),0)||<center>x,y</center> | ||
| + | |- | ||
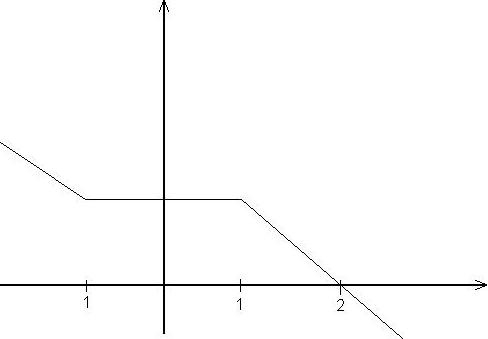
| + | |<center>9</center>||Вычислить значение функции, заданной графически, по заданному значению аргумента х [[Изображение:рис1.JPG|center]]||<center>x</center> | ||
| + | |- | ||
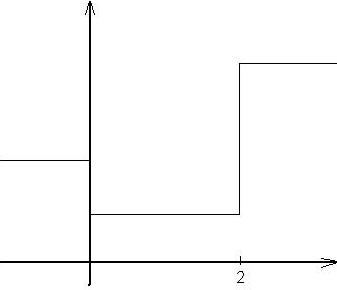
| + | |<center>10</center>||Вычислить значение функции, заданной графически, по заданному значению аргумента х [[Изображение:рис2.JPG|center]]|| | ||
| + | |- | ||
| + | |<center>11</center>||Решить линейное уравнение ax+b=0 для любых значений коэффициентов.||<center>a,b</center> | ||
| + | |- | ||
| + | |<center>12</center>||Проверить, делится ли выбранное числона 5, на 11 или 13.||<center>x</center> | ||
| + | |- | ||
| + | |<center>13</center>||Определить, является ли сумма цифр четырехзначного числа четной||<center>m</center> | ||
| + | |- | ||
| + | |<center>14</center>||Проверить, кратно ли заданное целое число и сумма его цифр 4||<center>n</center> | ||
| + | |||
| + | |} | ||
| + | |||
| + | ==Литература == | ||
#Архангельский. Программирование на Delphi 6. – М: БИНОМ, 2002 | #Архангельский. Программирование на Delphi 6. – М: БИНОМ, 2002 | ||
#Бобровский С. Delphi 7. Учебный курс. – СПб: Питер, 2003 | #Бобровский С. Delphi 7. Учебный курс. – СПб: Питер, 2003 | ||
#Культин Н. Основы программирования в Delphi 7. СПб: БХВ-Петербург, 2005. | #Культин Н. Основы программирования в Delphi 7. СПб: БХВ-Петербург, 2005. | ||
| + | |||
| + | ==Ссылки== | ||
| + | |||
| + | [[Учебный курс Программирование на Delphi]] | ||
| + | |||
| + | [[Учебный план курса Программирование на Delphi]] | ||
| + | |||
| + | |||
[[Категория: Учебный курс Программирование на Delphi]] | [[Категория: Учебный курс Программирование на Delphi]] | ||
Текущая версия на 07:20, 19 апреля 2008
Содержание
Оператор If
Алгоритм называется разветвляющимся, если он содержит несколько ветвей, отличающихся друг от друга содержанием вычислений. Выход вычислительного процесса на ту или иную ветвь алгоритма определяется исходными данными задачи.
Пример 1
- Условие задачи
Найти максимальную из двух величин а и в
- Использованные компоненты
Edit1 – для ввода первого числа
Edit2 – для ввода второго числа
Label1 - для вывода описания
Label2 - для вывода описания
Label3 - для вывода результирующего сопротивления
BitBtn1 - для запуска решения
BitBtn2 - для выхода из формы
- Программный код
unit Unit1;
interface uses Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, Dialogs, StdCtrls, Buttons;
type TForm1 = class(TForm) Label1: TLabel; Label2: TLabel; Edit1: TEdit; Edit2: TEdit; Label3: TLabel; BitBtn1: TBitBtn; BitBtn2: TBitBtn; procedure BitBtn2Click(Sender: TObject); procedure BitBtn1Click(Sender: TObject); private { Private declarations } public { Public declarations } end;
var Form1: TForm1;
implementation
{$R *.dfm} var a,b,m:real; procedure TForm1.BitBtn2Click(Sender: TObject); begin Close; end;
procedure TForm1.BitBtn1Click(Sender: TObject); begin a:=strtofloat(edit1.Text); b:=strtofloat(edit2.Text); if a>=b then m:=a else m:=b;
label3.caption:='Первое число= '+floattostr(a)+#13+'Второе число= ' +floattostr(b)+#13+'Максимальное= '+floattostr(m); end;
end.
- Форма с результатом работы программы
Задание
Таблица 5
| Номер варианта | Условие | Исходные данные | |
|---|---|---|---|
| Три точки на плоскости заданы своими координатами.Выяснить какие из них находятся на максимальном расстоянии друг от друга | |||
| Вычислить: max^3(a,b,c)+min^2(a,b,c) | |||
| Заданы три величины а, b, c. Определить максимальное и минимальное значение из их среднего геометрического, среднего арифметического и суммы экспонент exp(a) + exp(b) + exp(c) | |||
| Определить в какой четверти координатной плоскости находится точка с координатами х,у | |||
| m=max(x,y,z) \ min ^ 2(a,b,c) | |||
| Z=min(0,x) - min(0,y) \ max ^ 2(y,x) | |||
| r=max(min(x,y),z)/3 | |||
| v=max(min(x-y,y-x),0) | |||
| Вычислить значение функции, заданной графически, по заданному значению аргумента х | |||
| Вычислить значение функции, заданной графически, по заданному значению аргумента х | |||
| Решить линейное уравнение ax+b=0 для любых значений коэффициентов. | |||
| Проверить, делится ли выбранное числона 5, на 11 или 13. | |||
| Определить, является ли сумма цифр четырехзначного числа четной | |||
| Проверить, кратно ли заданное целое число и сумма его цифр 4 |
Литература
- Архангельский. Программирование на Delphi 6. – М: БИНОМ, 2002
- Бобровский С. Delphi 7. Учебный курс. – СПб: Питер, 2003
- Культин Н. Основы программирования в Delphi 7. СПб: БХВ-Петербург, 2005.