Учебный курс Программирование на Delphi. Модуль 7: различия между версиями
(→Задание) |
|||
| (не показана 1 промежуточная версия 1 участника) | |||
| Строка 198: | Строка 198: | ||
==Задание== | ==Задание== | ||
| − | + | Таблица 9(Находится в разработке) | |
| − | + | Таблица 10(Находится в разработке) | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Литература== | ==Литература== | ||
Текущая версия на 09:01, 19 апреля 2008
Содержание
Операторы REPEAT и WHILE
Для программирования циклов с условием в Delphi существуют оператор цикла с предусловием WHILE и оператор цикла с постусловием REPEAT.
Формат операторов:
while условие do оператор;
repeat операторы until условие;
условие – логическое выражение.
В операторе while сначала вычисляется логическое выражение и если оно истинно, то выполняется оператор. После этого управление возвращается в начало цикла на вычисление логического выражения. Если условие ложно, оператор завершает работу и управление передаётся на следующий оператор.
В операторе repeat сначала выполняются операторы, и только потом вычисляется логическое выражение. Если оно ложно, то управление возвращается в начало цикла, повторяется выполнение операторов тела цикла. Если условие истинно – то выход из цикла.
Пример 1.
- Условие
Алгоритм Евклида для подсчета НОД (наибольшего общего делителя) двух натуральных чисел.
- Использованные компоненты
Label1 - для вывода описания
Label2 - для вывода описания
Label3 - для вывода описания
Edit2 - для ввода числа
Edit1 - для ввода числа
BitBtn1 - для запуска решения
BitBtn2 - для выхода из формы
- Программный код
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Buttons;
type
TForm1 = class(TForm)
Label1: TLabel;
Label2: TLabel;
Edit2: TEdit;
Label3: TLabel;
BitBtn1: TBitBtn;
BitBtn2: TBitBtn;
Edit1: TEdit;
procedure BitBtn2Click(Sender: TObject);
procedure BitBtn1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
var
a,b,x,y,z:integer;
procedure TForm1.BitBtn2Click(Sender: TObject);
begin
close;
end;
procedure TForm1.BitBtn1Click(Sender: TObject);
begin
a:=strtoint(edit1.Text);
b:=strtoint(edit2.Text);
x:=a; y:=b;
while (x<>y) do
if x>y then x:=x-y
else y:=y-x;
z:=x;
label3.Caption:='НОД= '+inttostr(z);
end;
end.
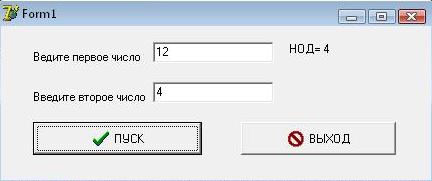
- Форма с результатом работы программы
Пример 2.
- Условие
Вычислить сумму членов ряда (...вставить формулу...) с точностью до члена ряда, меньшего Е.
- Использованные компоненты
Label1 - для тектовых коментарий;
Label2 - для вывода результата;
Edit1 - для ввода числа;
BitBtn1 - для запуска программы;
BitBtn2 - для выхода из программы.
- Программный код
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Buttons;
type
TForm1 = class(TForm)
Label1: TLabel;
Label2: TLabel;
Edit1: TEdit;
BitBtn1: TBitBtn;
BitBtn2: TBitBtn;
procedure BitBtn2Click(Sender: TObject);
procedure BitBtn1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
var n:integer;
s,z,e:real;
procedure TForm1.BitBtn2Click(Sender: TObject);
begin
close;
end;
procedure TForm1.BitBtn1Click(Sender: TObject);
begin
e:=strtofloat(edit1.Text);
n:=1; z:=1/6; s:=0;
while abs(z)>=e do
begin
s:=s+z;
n:=n+1;
z:=n/((n+1)*(n+2));
end;
label2.Caption:='Сумма= '+floattostr(s);
end;
end.
- Форма с результатом работы программы
Пример 3.
- Условие
Вычислить кубический корень из числа m методом Ньютона по формуле: ...(вставить формулу)... Вычисления продолжать пока ...(вставить формулу)... не станет меньше заданной точности Е.
- Использованные компоненты
Label1 - для текстовых комментарий;
Label2 - для текстовых комментарий;
Label3 - для вывода результата;
Edit1 - для ввода числа;
Edit2 - для ввода числа;
BitBtn1 - для запуска программы;
BitBtn2 -для выхода из программы.
- Программный код
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Buttons;
type
TForm1 = class(TForm)
Label1: TLabel;
Label2: TLabel;
Edit1: TEdit;
Edit2: TEdit;
Label3: TLabel;
BitBtn1: TBitBtn;
BitBtn2: TBitBtn;
procedure BitBtn2Click(Sender: TObject);
procedure BitBtn1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
var x1,x2,d,e,m:real;
procedure TForm1.BitBtn2Click(Sender: TObject);
begin
close;
end;
procedure TForm1.BitBtn1Click(Sender: TObject);
begin
m:=strtofloat(edit1.Text);
e:=strtofloat(edit2.Text);
x1:=m;
repeat
x2:=2/3*x1+m/3/sqr(x1);
d:=abs(x1-x2);
x1:=x2;
until d<=e;
label3.Caption:='Корень= '+floattostr(x2);
end;
end.
- Форма с результатом работы программы
Задание
Таблица 9(Находится в разработке)
Таблица 10(Находится в разработке)
Литература
- Архангельский. Программирование на Delphi 6. – М: БИНОМ, 2002
- Бобровский С. Delphi 7. Учебный курс. – СПб: Питер, 2003
- Культин Н. Основы программирования в Delphi 7. СПб: БХВ-Петербург, 2005.