Учебный курс Программирование на Delphi. Модуль 14

Использование функций

Использование функций

Функция отличается от процедуры тем, что результат ее работы возвращается в виде значения этой функции и, следовательно, вызов функции может использоваться наряду с другими операндами выражения. Рекурсия - такой способ организации вычислительного процесса, при котором подпрограмма в ходе выполнения составляющих ее операторов обращается сама к себе.

Пример 1.

• Условие задачи:

Даны все действительные числа a,b,c.Вычислить max(a,b,+c)+max(a+b,c)/1+max(a+bc,12)

• Использованные компоненты:

Label1 - используется для текстовых комментариев;

Label2 - используется для вывода суммы;

edit1 - используется для ввода числа;

edit2 - используется для ввода числа;

edit3 - используется для ввода числа;

BitBtn1 - запуск программы;

BitBtn2 - выход из программы;

• Программный код:

 unit Unit2;
 interface
 uses
 Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
 Dialogs, StdCtrls, ExtCtrls, Grids, XPMan, Buttons;
 type
 TForm1 = class(TForm)
   Edit1: TEdit;
   Edit2: TEdit;                
   Edit3: TEdit;
   Label1: TLabel;
   Label2: TLabel;
   Label3: TLabel;
   Label4: TLabel;
   Label5: TLabel;
   XPManifest1: TXPManifest;
   BitBtn1: TBitBtn;
   BitBtn2: TBitBtn;
   procedure BitBtn2Click(Sender: TObject);
   procedure BitBtn1Click(Sender: TObject);
 private
   { Private declarations }
 public
   { Public declarations }
 end;
 var
 Form1: TForm1;
 implementation
 {$R *.dfm}
 function max (x,y: real): real;
    begin
        if x > y
           then  max:=x
           else  max:=y
    end;
  var z, a, b, c: real;
 procedure TForm1.BitBtn2Click(Sender: TObject);
 begin
 begin
     a:=strtoint(edit1.Text);
     b:=strtoint(edit2.text);
     c:=strtoint(edit3.Text);
     z:=(max(a, b+c) + max(a+b, c*c))/(1+ max(a+b*c, 12));
     Label4.Caption:=floattostr(z);
    end;
    end;
 procedure TForm1.BitBtn1Click(Sender: TObject);
 begin
 close;
 end;
 end.

• Форма с результатом работы программы:

Пример 2.

• Условие задачи:

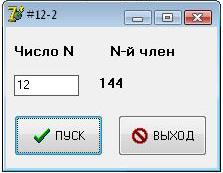
Найти N число последовательности Фибоначчи. Использовать рекурсивную функцию. Числа Фибоначчи образуют последовательность, у которой каждый очередной член равен сумме двух предыдущих: 0 1 1 2 3 5 8 13 . . . Обозначив N-й член ряда Фибоначчи F(N), можно записать следующую рекурсивную зависимость: F(N) = F(N - 1) + F(N - 2), n >= 3, F(1) = 1 и F(2) = 1

• Использованные компоненты:

Label1 - используется для текстовых комментариев;

Label2 - используется для текстовых комментариев;

edit1 - используется для ввода числа;

BitBtn1 - запуск программы;

BitBtn2 - выход из программы;

• Программный код:

unit Unit1;
interface
uses
 Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
 Dialogs, XPMan, StdCtrls, Buttons;
type
 TForm1 = class(TForm)
   Edit1: TEdit;
   Label1: TLabel;
   Label2: TLabel;
   XPManifest1: TXPManifest;
   Label3: TLabel;
   BitBtn1: TBitBtn;
   BitBtn2: TBitBtn;
   procedure BitBtn1Click(Sender: TObject);
   procedure BitBtn2Click(Sender: TObject);
 private
   { Private declarations }
 public
   { Public declarations }
 end;
var
 Form1: TForm1;
implementation
{$R *.dfm}
function F(k: integer): integer;
begin 
    if (k=1) or (k=2)
           then F:=1
           else F:= F(k-1) + F(k-2)
end;
procedure TForm1.BitBtn1Click(Sender: TObject);
var N: integer;
begin
N:=strtoint(Edit1.Text);
label2.Caption:=inttostr(F(n));
end;
procedure TForm1.BitBtn2Click(Sender: TObject);
begin
close;
end;
end.

• Форма с результатом работы программы:

Задание

Таблица 20

Номер варианта	Условие
1	Вычислить число сочетаний из n по m(n>m) по формуле:Файл:Задание14 вар1.JPG
2	Вычислить: Файл:Задание14 вар2.JPG
3	Вычислить: Файл:Задание14 вар3.JPG
4	Найти все трехзначные числа, равные сумме факториалов своих цифр.
5	Два треугольника заданы координатами своих вершин. Вычислить площади треугольников с помощью формулы Герона и определить, какой треугольник имеет большую площадь.
6	Решить уравнение: ax + b = 0, где Значения k, l, m вводятся.
7	Даны действительные числа s,t. Вычислить: где
8	Вычислить число сочетаний с повторениями по формуле:
9	Найти наибольший общий делитель целых положительных чисел a, b, c.
10	Даны действительные числа х, у. Вычислить: где
11	Решить уравнение: Файл:Задание14 вар11(1).JPG , где Значения r, m, n вводятся.
12	Используя функцию нахождения наибольшего общего делителя, найти наименьшее общее кратное двух чисел.
13	Вычислить:
14	Вычислить:

Таблица 21

Номер варианта	Условие
1	Найти НОД двух неотрицательных целых чисел m и n с использованием первого алгоритма Евклида:
2	Найти НОД двух неотрицательных целых чисел m и n c использованием второго алгоритма Евклида:
3	Вычислить функцию Аккермана A(n, m) для неотрицательных целых чисел m и n по формуле:
4	Вычислить числа Каталана K(n) для натурального n по формуле: K(1) = K(2) = 1 K(n) = K(n - 1)*(4*n - 6)/n, при n * 3
5	Вычислить n-ый член арифметической прогрессии. Заданы первый член а1 и разность d.
6	Вычислить n-ый член геометрической прогрессии. Заданы первый член а1 и знаменатель геометрической прогрессии q.
7	Вычислить сумму n членов арифметической прогрессии. Заданы первый член а1 и разность d. Для вычисления члена арифметической прогрессии использовать формулу варианта 5.
8	Вычислить сумму n членов геометрической прогрессии. Заданы первый член а1 и знаменатель геометрической прогрессии q. Для вычисления члена геометрической прогрессии использовать формулу варианта 6.
9	Вычислить: Для вычисления факториала воспользоваться формулой:
10	Найти максимум из двух величин НОД(a, b) и НОД(c, d). Для вычисления наибольшего общего делителя воспользоваться формулой варианта 1.
11	Вычислить a!+b!. Для вычисления факториала воспользоваться формулой варианта 9.
12	Вычислить F(k) -F(m), где F(k) - k-ый член последовательности Фибоначчи, F(m) - m-ый член последовательности Фибоначчи. F(1) = F(2) = 1 F(n) = F(n-1) + F(n-2) для n >= 3
13	Вычислить: Для вычисления наибольшего общего делителя воспользоваться формулой варианта 2.
14	Вычислить величину pow(x, n) для вещественного х<>0 и целого n по формуле:

Литература

1. Архангельский. Программирование на Delphi 6. – М: БИНОМ, 2002
2. Бобровский С. Delphi 7. Учебный курс. – СПб: Питер, 2003
3. Культин Н. Основы программирования в Delphi 7. СПб: БХВ-Петербург, 2005.

Ссылки

Учебный курс Программирование на Delphi

Учебный план курса Программирование на Delphi