Математическое моделирование: различия между версиями
| Строка 4: | Строка 4: | ||
'''Математическое моделирование''' - это средство изучения реального объекта, процесса или системы путем их замены математической моделью, более удобной для экспериментального исследования с помощью ЭВМ. | '''Математическое моделирование''' - это средство изучения реального объекта, процесса или системы путем их замены математической моделью, более удобной для экспериментального исследования с помощью ЭВМ. | ||
| + | Виды моделирования | ||
| + | |||
| + | *Информационное моделирование | ||
| + | *Компьютерное моделирование | ||
| + | *Математическое моделирование | ||
| + | *Математико-картографическое моделирование | ||
| + | *Молекулярное моделирование | ||
| + | *Цифровое моделирование | ||
| + | *Логическое моделирование | ||
| + | *Педагогическое моделирование | ||
| + | *Психологическое моделирование | ||
| + | *Статистическое моделирование | ||
| + | *Структурное моделирование | ||
| + | *Физическое моделирование | ||
| + | *Экономико-математическое моделирование | ||
| + | *Имитационное моделирование | ||
| + | *Эволюционное моделирование | ||
| + | |||
| + | Источник: http://5fan.ru/wievjob.php?id=26378 | ||
| + | |||
Версия 12:27, 10 января 2017
Математическая модель является приближенным представлением реальных объектов, процессов или систем, выраженным в математических терминах и сохраняющим существенные черты оригинала.
Математические модели в количественной форме, с помощью логико-математических конструкций, описывают основные свойства объекта, процесса или системы, его параметры, внутренние и внешние связи.
Математическое моделирование - это средство изучения реального объекта, процесса или системы путем их замены математической моделью, более удобной для экспериментального исследования с помощью ЭВМ.
Виды моделирования
- Информационное моделирование
- Компьютерное моделирование
- Математическое моделирование
- Математико-картографическое моделирование
- Молекулярное моделирование
- Цифровое моделирование
- Логическое моделирование
- Педагогическое моделирование
- Психологическое моделирование
- Статистическое моделирование
- Структурное моделирование
- Физическое моделирование
- Экономико-математическое моделирование
- Имитационное моделирование
- Эволюционное моделирование
Источник: http://5fan.ru/wievjob.php?id=26378
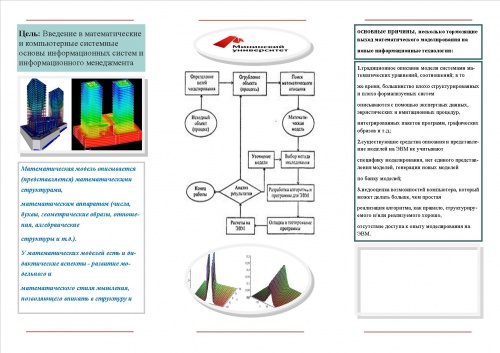
Этапы и принципы построения математических моделей
Процесс разработки математических моделей состоит из следующих этапов:
- формулирование проблемы;
- определение цели моделирования;
- организация и проведение исследования предметной области (исследование свойств объекта моделирования);
- разработка модели;
- проверка ее точности и соответствия реальности;
- практическое использование, т.е. перенос полученных с помощью модели знаний на исследуемый объект или процесс.

В основу классификации математических моделей можно положить различные принципы. Можно классифицировать модели по отраслям наук (математические модели в физике, биологии, социологии и т.д.). Можно классифицировать по применяемому математическому аппарату (модели, основанные на применении обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, стохастических методов, дискретных алгебраических преобразований и т.д.). Наконец, если исходить из общих задач моделирования в разных науках безотносительно к математическому аппарату, наиболее естественна такая классификация:
1. дескриптивные (описательные) модели; 2. оптимизационные модели; 3. многокритериальные модели; 4. игровые модели.
Еще один подход к классификации математических моделей подразделяет их на детерминированные и стохастические (вероятностные). В детерминированных моделях входные параметры поддаются измерению однозначно и с любой степенью точности, т.е. являются детерминированными величинами.Соответственно, процесс эволюции такой системы детерминирован. В стохастических моделях значения входных параметров известны лишь с определенной степенью вероятности, т.е. эти параметры являются стохастическими; соответственно, случайным будет и процесс эволюции системы. При этом, выходные параметры стохастической модели могут быть как величинами вероятностными, так и однозначно определяемыми.
Наконец, если ограничиться непрерывными детерминистскими моделями, то их часто подразделяют на системы с сосредоточенными параметрами и системы с распределенными параметрами. Системы с сосредоточенными параметрами описываются с помощью конечного числа обыкновенных дифференциальных уравнений для зависящих от времени переменных. Пространство состояний имеет здесь конечную размерность (число степеней свободы системы конечно). В противоположность этому под системами с распределенными параметрами понимают системы, описываемые конечным числом дифференциальных уравнений в частных производных. Здесь переменные состояния в каждый момент времени есть функции одной или нескольких пространственных переменных. Пространство состояний имеет в этом случае бесконечную размерность, т.е. система обладает бесконечным числом степеней свободы.