Математическое моделирование: различия между версиями
| (не показано 7 промежуточных версий этого же участника) | |||
| Строка 4: | Строка 4: | ||
'''Математическое моделирование''' - это средство изучения реального объекта, процесса или системы путем их замены математической моделью, более удобной для экспериментального исследования с помощью ЭВМ. | '''Математическое моделирование''' - это средство изучения реального объекта, процесса или системы путем их замены математической моделью, более удобной для экспериментального исследования с помощью ЭВМ. | ||
| + | '''Виды моделирования''' | ||
| − | + | *Информационное моделирование | |
| + | *Компьютерное моделирование | ||
| + | *Математическое моделирование | ||
| + | *Математико-картографическое моделирование | ||
| + | *Молекулярное моделирование | ||
| + | *Цифровое моделирование | ||
| + | *Логическое моделирование | ||
| + | *Педагогическое моделирование | ||
| + | *Психологическое моделирование | ||
| + | *Статистическое моделирование | ||
| + | *Структурное моделирование | ||
| + | *Физическое моделирование | ||
| + | *Экономико-математическое моделирование | ||
| + | *Имитационное моделирование | ||
| + | *Эволюционное моделирование | ||
| + | '''ИНФОРМАЦИОННОЕ''' | ||
| + | В своей деятельности человек повсеместно использует модели, то есть создает образ, копию того объекта, с которым ему приходится иметь дело. Продумывая план действий, представляя результат своих действий, человек строит модель на уровне мысли. | ||
| + | Модель - это искусственно созданный объект, дающий упрощенное представление о реальном объекте, процессе или явлении, отражающий существенные стороны изучаемого объекта с точки зрения цели моделирования. Моделирование - это построение моделей, предназначенных для изучения и исследования объектов, процессов или явлений. | ||
| + | Объект, для которого создается модель, называют оригиналом или прототипом. Любая модель не является абсолютной копией своего оригинала, она лишь отражает некоторые его качества и свойства, наиболее существенные для выбранной цели исследования. При создании модели всегда присутствуют определенные допущения и гипотезы. | ||
| + | Системный подход позволяет создавать полноценные модели. Особенности системного подхода заключаются в следующем. Изучаемый объект рассматривается как система, описание и исследование элементов которой не выступает как сама цель, а выполняется с учетом их места (наличие подзадач). В целом объект не отделяется от условий его существования и функционирования. Объект рассматривается как составная часть чего-то целого (сам является подзадачей). Один и тот же исследуемый элемент рассматривается как обладающий разными характеристиками, функциями и даже принципами построения. При системном подходе на первое место выступают не только причинные объяснения функционирования объекта, но и целесообразность включения его в состав других элементов. Допускается возможность наличия у объекта множества индивидуальных характеристик и степеней свободы. Альтернативы решения задач сравниваются в первую очередь по критерию "стоимость-эффективность". | ||
| − | Этапы и принципы построения математических моделей | + | '''КОМПЬЮТЕРНОЕ''' |
| + | Создание универсальных моделей - это следствие использование системного подхода. | ||
| + | Моделирование (эксперимент) может быть незаменимо. Мы не можем, например, устроить ядерную катастрофу, чтобы выяснить масштабы возможного заражения, а с помощью компьютера возможен расчет (и достаточно точный) интересующих исследователей параметров. | ||
| + | Моделирование - исследование явлений, процессов или систем объектов путем построения и изучения их моделей - это основной способ научного познания. В информатике данный способ называется вычислительный эксперимент и основывается он на трех основных понятиях: модель - алгоритм - программа. Использование компьютера при моделировании возможно по трем направлениям: | ||
| + | 1. Вычислительное - прямые расчеты по программе. | ||
| + | 2. Инструментальное - построение базы знаний, для преобразования ее в алгоритм и программу. | ||
| + | 3. Диалоговое - поддержание интерфейса между исследователем и компьютером. | ||
| + | |||
| + | '''ФИЗИЧЕСКОЕ''' | ||
| + | Метод экспериментального изучения различных физических явлений, основанный на их физическом подобии. | ||
| + | Метод применяется при следующих условиях: Исчерпывающе точного математического описания явления на данном уровне развития науки не существует, или такое описание слишком громоздко и требует для расчётов большого объёма исходных данных, получение которых затруднительно. | ||
| + | Воспроизведение исследуемого физического явления в целях эксперимента в реальных масштабах невозможно, нежелательно, или слишком дорогостояще. (Например, цунами) Некоторые примеры применения метода физического моделирования: | ||
| + | Исследование течений газов и обтекания летательных аппаратов, автомобилей, и т.п. в аэродинамических трубах. | ||
| + | Гидродинамические исследования на уменьшенных моделях кораблей, гидротехнических сооружений и т.п. | ||
| + | Исследование сейсмоустойчивости зданий и сооружений на этапе проектирования. | ||
| + | Изучение устойчивости сложных конструкций, под воздействием сложных силовых нагрузок. | ||
| + | Измерение тепловых потоков и рассеивания тепла в устройствах и системах, работающих в условиях больших тепловых нагрузок. | ||
| + | Изучение стихийных явлений и их последствий. | ||
| + | |||
| + | '''МАТЕМАТИЧЕСКОЕ''' | ||
| + | Это модель, созданная с помощью математических понятий. | ||
| + | Математическое моделирование — процесс построения и изучения математических моделей. | ||
| + | Все естественные и общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием: заменяют реальный объект его моделью и затем изучают последнюю. | ||
| + | |||
| + | '''ПЕДАГОГИЧЕСКОЕ''' | ||
| + | Разработка и создание формальной модели педагогического процесса или его составляющих, отражающей основные идеи, методы, формы, средства, приемы и технологические решения, которые подлежат в дальнейшем экспериментальному изучению в условиях реального педагогического процесса. ПСИХОЛОГИЧЕСКОЕ Создание формальной модели психического или социально-психологического процесса, т.е. формализованной абстракции данного процесса, воспроизводящей его некоторые основные, ключевые, по мнению данного исследователя, моменты с целью его экспериментального изучения либо с целью экстраполяции сведений о нём на то, что исследователь считает частными случаями данного процесса. | ||
| + | В настоящее время в психологии всё чаще используются модели, основанные на вероятностно-статистической оценке явлений и алгоритмическом подходе. | ||
| + | |||
| + | '''ЭКОНОМИКО-МАТЕМАТИЧЕСКОЕ''' | ||
| + | (один из разделов математических методов в экономике, наравне с эконометрикой) — сфера научной и практической деятельности, целью которой является математически формализованное описание экономических объектов, процессов и явлений. | ||
| + | Математика как основа теории принятия решений широко применяется для управления (планирования, прогнозирования, контроля) экономическими объектами и процессами. Например, прогнозы социально-экономического развития РФ, разрабатываемые МЭРТ, основаны на математическом анализе ретроспективных показателей (динамики инфляции, ВВП и т. д.) и строятся с применением таких разделов эконометрики и прикладной статистики, как корреляционный анализ, регрессионный анализ, метод главных компонент, факторный анализ и т. д. | ||
| + | Новым направлением в современной экономической науке является реализация так называемого экономического эксперимента, суть которого заключается в математическом моделировании экономических ситуаций с учётом психологического фактора (ожиданий участников рынка). | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''''Этапы и принципы построения математических моделей''''' | ||
Процесс разработки математических моделей состоит из следующих этапов: | Процесс разработки математических моделей состоит из следующих этапов: | ||
| Строка 22: | Строка 79: | ||
- практическое использование, т.е. перенос полученных с помощью модели знаний на исследуемый объект или процесс. | - практическое использование, т.е. перенос полученных с помощью модели знаний на исследуемый объект или процесс. | ||
| + | [[Изображение:Буклет Борисов и Косов1.jpg|500px]] | ||
| + | [[Изображение:Буклет Борисов и Косов2.jpg|500px]] | ||
| − | + | В основу классификации математических моделей можно положить различные принципы. Можно классифицировать модели по отраслям наук (математические модели в физике, биологии, социологии и т.д.). Можно классифицировать по применяемому математическому аппарату (модели, основанные на применении обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, стохастических методов, дискретных алгебраических преобразований и т.д.). Наконец, если исходить из общих задач моделирования в разных науках безотносительно к математическому аппарату, наиболее естественна такая классификация: | |
1. дескриптивные (описательные) модели; | 1. дескриптивные (описательные) модели; | ||
| Строка 30: | Строка 89: | ||
4. игровые модели. | 4. игровые модели. | ||
| − | + | Еще один подход к классификации математических моделей подразделяет их на детерминированные и стохастические (вероятностные). | |
| + | В детерминированных моделях входные параметры поддаются измерению однозначно и с любой степенью точности, т.е. являются детерминированными величинами.Соответственно, процесс эволюции такой системы детерминирован. | ||
| + | В стохастических моделях значения входных параметров известны лишь с определенной степенью вероятности, т.е. эти параметры являются стохастическими; соответственно, случайным будет и процесс эволюции системы. При этом, выходные параметры стохастической модели могут быть как величинами вероятностными, так и однозначно определяемыми. | ||
| + | |||
| + | Наконец, если ограничиться непрерывными детерминистскими моделями, то их часто подразделяют на системы с сосредоточенными параметрами и системы с распределенными параметрами. Системы с сосредоточенными параметрами описываются с помощью конечного числа обыкновенных дифференциальных уравнений для зависящих от времени переменных. Пространство состояний имеет здесь конечную размерность (число степеней свободы системы конечно). В противоположность этому под системами с распределенными параметрами понимают системы, описываемые конечным числом дифференциальных уравнений в частных производных. Здесь переменные состояния в каждый момент времени есть функции одной или нескольких пространственных переменных. Пространство состояний имеет в этом случае бесконечную размерность, т.е. система обладает бесконечным числом степеней свободы. | ||
| + | == Полезные ресурсы == | ||
| + | |||
| + | |||
| + | [http://koi.tspu.ru/koi_books/gazizov/l7p01.htm Компьютерное и математическое моделирование] | ||
| + | |||
| + | [http://www.shapovalov.org/load/8-1-0-45 Математическое и компьютерное моделирование ] | ||
| + | |||
| + | [http://bourabai.ru/library/mcm11.pdf Лекция: Математическое и компьютерное моделирование] | ||
| + | |||
| + | [http://www.inf1.info/book/export/html/215 Компьютерное моделирование] | ||
| − | + | == Проекты с аналогичной тематикой == | |
| + | [http://wiki.iteach.ru/index.php/%22%D0%92%D0%B5%D1%81%D1%8C_%D0%BC%D0%B8%D1%80_%D0%BD%D0%B0_%D0%BE%D0%B4%D0%BD%D0%BE%D0%B9_%D0%BB%D0%B0%D0%B4%D0%BE%D0%BD%D0%B8%22#.D0.92.D0.BE.D0.BF.D1.80.D0.BE.D1.81.D1.8B.2C_.D0.BD.D0.B0.D0.BF.D1.80.D0.B0.D0.B2.D0.BB.D1.8F.D1.8E.D1.89.D0.B8.D0.B5_.D0.BF.D1.80.D0.BE.D0.B5.D0.BA.D1.82 "Весь мир на одной ладони"] | ||
Текущая версия на 12:39, 10 января 2017
Математическая модель является приближенным представлением реальных объектов, процессов или систем, выраженным в математических терминах и сохраняющим существенные черты оригинала.
Математические модели в количественной форме, с помощью логико-математических конструкций, описывают основные свойства объекта, процесса или системы, его параметры, внутренние и внешние связи.
Математическое моделирование - это средство изучения реального объекта, процесса или системы путем их замены математической моделью, более удобной для экспериментального исследования с помощью ЭВМ.
Виды моделирования
- Информационное моделирование
- Компьютерное моделирование
- Математическое моделирование
- Математико-картографическое моделирование
- Молекулярное моделирование
- Цифровое моделирование
- Логическое моделирование
- Педагогическое моделирование
- Психологическое моделирование
- Статистическое моделирование
- Структурное моделирование
- Физическое моделирование
- Экономико-математическое моделирование
- Имитационное моделирование
- Эволюционное моделирование
ИНФОРМАЦИОННОЕ В своей деятельности человек повсеместно использует модели, то есть создает образ, копию того объекта, с которым ему приходится иметь дело. Продумывая план действий, представляя результат своих действий, человек строит модель на уровне мысли. Модель - это искусственно созданный объект, дающий упрощенное представление о реальном объекте, процессе или явлении, отражающий существенные стороны изучаемого объекта с точки зрения цели моделирования. Моделирование - это построение моделей, предназначенных для изучения и исследования объектов, процессов или явлений. Объект, для которого создается модель, называют оригиналом или прототипом. Любая модель не является абсолютной копией своего оригинала, она лишь отражает некоторые его качества и свойства, наиболее существенные для выбранной цели исследования. При создании модели всегда присутствуют определенные допущения и гипотезы. Системный подход позволяет создавать полноценные модели. Особенности системного подхода заключаются в следующем. Изучаемый объект рассматривается как система, описание и исследование элементов которой не выступает как сама цель, а выполняется с учетом их места (наличие подзадач). В целом объект не отделяется от условий его существования и функционирования. Объект рассматривается как составная часть чего-то целого (сам является подзадачей). Один и тот же исследуемый элемент рассматривается как обладающий разными характеристиками, функциями и даже принципами построения. При системном подходе на первое место выступают не только причинные объяснения функционирования объекта, но и целесообразность включения его в состав других элементов. Допускается возможность наличия у объекта множества индивидуальных характеристик и степеней свободы. Альтернативы решения задач сравниваются в первую очередь по критерию "стоимость-эффективность".
КОМПЬЮТЕРНОЕ Создание универсальных моделей - это следствие использование системного подхода. Моделирование (эксперимент) может быть незаменимо. Мы не можем, например, устроить ядерную катастрофу, чтобы выяснить масштабы возможного заражения, а с помощью компьютера возможен расчет (и достаточно точный) интересующих исследователей параметров. Моделирование - исследование явлений, процессов или систем объектов путем построения и изучения их моделей - это основной способ научного познания. В информатике данный способ называется вычислительный эксперимент и основывается он на трех основных понятиях: модель - алгоритм - программа. Использование компьютера при моделировании возможно по трем направлениям: 1. Вычислительное - прямые расчеты по программе. 2. Инструментальное - построение базы знаний, для преобразования ее в алгоритм и программу. 3. Диалоговое - поддержание интерфейса между исследователем и компьютером.
ФИЗИЧЕСКОЕ Метод экспериментального изучения различных физических явлений, основанный на их физическом подобии. Метод применяется при следующих условиях: Исчерпывающе точного математического описания явления на данном уровне развития науки не существует, или такое описание слишком громоздко и требует для расчётов большого объёма исходных данных, получение которых затруднительно. Воспроизведение исследуемого физического явления в целях эксперимента в реальных масштабах невозможно, нежелательно, или слишком дорогостояще. (Например, цунами) Некоторые примеры применения метода физического моделирования: Исследование течений газов и обтекания летательных аппаратов, автомобилей, и т.п. в аэродинамических трубах. Гидродинамические исследования на уменьшенных моделях кораблей, гидротехнических сооружений и т.п. Исследование сейсмоустойчивости зданий и сооружений на этапе проектирования. Изучение устойчивости сложных конструкций, под воздействием сложных силовых нагрузок. Измерение тепловых потоков и рассеивания тепла в устройствах и системах, работающих в условиях больших тепловых нагрузок. Изучение стихийных явлений и их последствий.
МАТЕМАТИЧЕСКОЕ Это модель, созданная с помощью математических понятий. Математическое моделирование — процесс построения и изучения математических моделей. Все естественные и общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием: заменяют реальный объект его моделью и затем изучают последнюю.
ПЕДАГОГИЧЕСКОЕ Разработка и создание формальной модели педагогического процесса или его составляющих, отражающей основные идеи, методы, формы, средства, приемы и технологические решения, которые подлежат в дальнейшем экспериментальному изучению в условиях реального педагогического процесса. ПСИХОЛОГИЧЕСКОЕ Создание формальной модели психического или социально-психологического процесса, т.е. формализованной абстракции данного процесса, воспроизводящей его некоторые основные, ключевые, по мнению данного исследователя, моменты с целью его экспериментального изучения либо с целью экстраполяции сведений о нём на то, что исследователь считает частными случаями данного процесса. В настоящее время в психологии всё чаще используются модели, основанные на вероятностно-статистической оценке явлений и алгоритмическом подходе.
ЭКОНОМИКО-МАТЕМАТИЧЕСКОЕ (один из разделов математических методов в экономике, наравне с эконометрикой) — сфера научной и практической деятельности, целью которой является математически формализованное описание экономических объектов, процессов и явлений. Математика как основа теории принятия решений широко применяется для управления (планирования, прогнозирования, контроля) экономическими объектами и процессами. Например, прогнозы социально-экономического развития РФ, разрабатываемые МЭРТ, основаны на математическом анализе ретроспективных показателей (динамики инфляции, ВВП и т. д.) и строятся с применением таких разделов эконометрики и прикладной статистики, как корреляционный анализ, регрессионный анализ, метод главных компонент, факторный анализ и т. д. Новым направлением в современной экономической науке является реализация так называемого экономического эксперимента, суть которого заключается в математическом моделировании экономических ситуаций с учётом психологического фактора (ожиданий участников рынка).
Этапы и принципы построения математических моделей
Процесс разработки математических моделей состоит из следующих этапов:
- формулирование проблемы;
- определение цели моделирования;
- организация и проведение исследования предметной области (исследование свойств объекта моделирования);
- разработка модели;
- проверка ее точности и соответствия реальности;
- практическое использование, т.е. перенос полученных с помощью модели знаний на исследуемый объект или процесс.

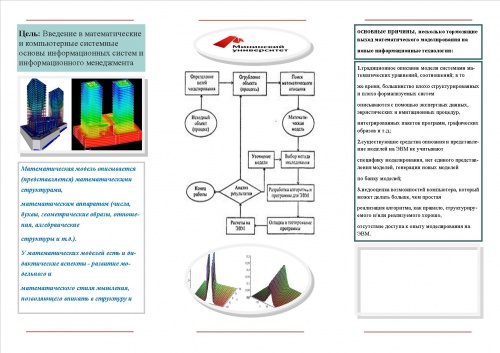
В основу классификации математических моделей можно положить различные принципы. Можно классифицировать модели по отраслям наук (математические модели в физике, биологии, социологии и т.д.). Можно классифицировать по применяемому математическому аппарату (модели, основанные на применении обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, стохастических методов, дискретных алгебраических преобразований и т.д.). Наконец, если исходить из общих задач моделирования в разных науках безотносительно к математическому аппарату, наиболее естественна такая классификация:
1. дескриптивные (описательные) модели; 2. оптимизационные модели; 3. многокритериальные модели; 4. игровые модели.
Еще один подход к классификации математических моделей подразделяет их на детерминированные и стохастические (вероятностные). В детерминированных моделях входные параметры поддаются измерению однозначно и с любой степенью точности, т.е. являются детерминированными величинами.Соответственно, процесс эволюции такой системы детерминирован. В стохастических моделях значения входных параметров известны лишь с определенной степенью вероятности, т.е. эти параметры являются стохастическими; соответственно, случайным будет и процесс эволюции системы. При этом, выходные параметры стохастической модели могут быть как величинами вероятностными, так и однозначно определяемыми.
Наконец, если ограничиться непрерывными детерминистскими моделями, то их часто подразделяют на системы с сосредоточенными параметрами и системы с распределенными параметрами. Системы с сосредоточенными параметрами описываются с помощью конечного числа обыкновенных дифференциальных уравнений для зависящих от времени переменных. Пространство состояний имеет здесь конечную размерность (число степеней свободы системы конечно). В противоположность этому под системами с распределенными параметрами понимают системы, описываемые конечным числом дифференциальных уравнений в частных производных. Здесь переменные состояния в каждый момент времени есть функции одной или нескольких пространственных переменных. Пространство состояний имеет в этом случае бесконечную размерность, т.е. система обладает бесконечным числом степеней свободы.
Полезные ресурсы
Компьютерное и математическое моделирование
Математическое и компьютерное моделирование
Лекция: Математическое и компьютерное моделирование