Результаты исследований учащихся в проекте Натуральные числа: различия между версиями
(→Вывод) |
Ксения23 (обсуждение | вклад) (→Полезные ресурсы) |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 55: | Строка 55: | ||
==Полезные ресурсы== | ==Полезные ресурсы== | ||
| + | |||
| + | Математика. 5 класс. Учебник. Мерзляк А.Г., Полонский В.Б., Якир М.С. | ||
| + | |||
| + | [http://realprojoe.com/istoriya-vozniknoveniya-naturalnyx-chisel/| История возникновения натуральных чисел] | ||
Текущая версия на 11:28, 7 мая 2014
Содержание
Авторы и участники проекта
- Земскова Ксения
- Груздева Антонина
- Участники группа "Историки"
Тема исследования группы
История возникновения натурального числа
Проблемный вопрос (вопрос для исследования)
Как возникло натуральное число?
Гипотеза исследования
Мы считаем, что натуральные числа нужны в повседневной жизни. Одно из их интереснейших сторон - это история её зарождения. Как они возникли? История натуральных чисел помогает нам не только лучше узнать математику, но и углубиться в причины её возникновения и просмотреть исторические моменты развития числовых знаний у наших предков.
Цели исследования
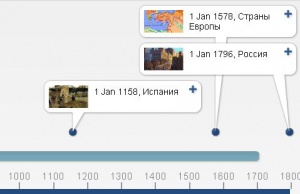
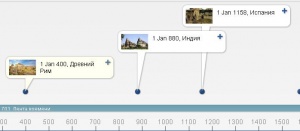
Познакомиться с историей возникновения натуральных чисел. Создать ленту времени.
Результаты проведённого исследования
Сначала были…пальцы. Весьма универсальное, удобное и сподручное средство для счёта. Его используют и до сих пор, правда, лишь в том случае, если нужно показать небольшое, ограниченное одним десятком число (здесь учитываем лишь возможности рук, пальцы ног не в счёт). Не удивительно, что очень быстро назрела потребность в других, более совершенных символах счёта.
У первобытных народов существовало развитой системы счисления. Еще в ХIХ веке у многих племен Австралии и Полинезии было только два обозначения - для числа "один" и для числа "два". Эти обозначения комбинировали. Число "три" они называли "два один", число "четыре"- "два и два", число "пять"- "два, два и один" , число "шесть"-"два, два и два". а числа, большие шести, они не различали и называли словом "много".
Первое подобие цифр возникло около пяти тысяч лет назад в Египте и Месопотамии и представляло собой засечки на дереве или камнях. Египетские жрецы использовали для письма папирус, а в Месопотамии для этих целей служила мягкая глина. Цифры тех времён обозначались чёрточками для единиц и различными другими метками для десятков и более высоких порядков.

Интересно то, что записи носили не только счётный характер, но и математический: древние египтяне, как известно, достигли потрясающих высот в арифметике и геометрии. Когда появились иероглифы, цифры стали записывать через них.
Следующий этап в истории цифр принадлежит древним римлянам. Изобретенная ими система исчисления основана на использовании букв для отображения чисел. Так, они применяли в своей системе буквы «I», «V», «L», «C», «D», и «M».
Не всем для записи чисел понадобилось столько символов. Например, майя в первом тысячелетии нашей эры писали любое число, используя лишь три знака: точку, линию и эллипс. Точка означала единицу, линия имела значение пяти, а эллипс, находясь под любым из этих знаков, увеличивал его значение в двадцать раз. Подобная минимизация отнюдь не приводила к упрощению записи: для обозначения того или иного числа приходилось использовать длинные ряды символов.
Современные привычные для нас цифры имеют арабское происхождение. Хотя арабы в свою очередь заимствовали их у индусов, видоизменив их и приспособив к своему письму. Характер написания каждой из девяти арабских цифр хорошо прослеживается, если записать их в «угловатой» форме. Количество углов каждой цифры соответствует количеству, которое эта цифра обозначает. Привычные нам формы цифр более округлые. Это влияние скорописи: так цифры записывать быстрее и удобнее.
Десятичная система, которой широко пользуется в настоящее время во всем мире, более совершенна. Вместо палочек, взятых от одной до девяти, используют цифры 1, 2, 3, 4, 5, 6, 7, 8, 9. Для обозначения десятков, сотен и т.д. не нужны новые значки, так как те же цифры используют и для записи десятков, сотен и т.д. Одна и та же цифра имеет различные значения в зависимости от места (позиции), где она записана. Благодаря этому свойству современную систему счисления называют позиционной. Десятичная позиционная система счисления позволяет записывать сколь угодно большие натуральные числа.
Народы пришли к этой системе постепенно. Она зародилась в Индии в V веке . В IХ веке ею уже владели арабы, в Х она дошла до Испании, а в ХII веке появилась в других странах Европы, но широкое распространение получила в ХVI веке. Долгое время развитие позиционной системы счисления тормозилось отсутствием в ней числа и цифры нуль. Только после введения нуля система стала совершенной.
В России десятичная система счисления начала распространяться в ХVII веке. В 1703 году был издан первый печатный учебник метематики - "Арифметика" Л. Ф. Магницкого, в котором все вычисления велись в десятичной системе записи чисел.
До этого числа записывали буквами славянского алфавита. Числа от 1 до 9 записывали так:

Над одной или несколькими буквами ставили особый знак (титло), чтобы подчеркнуть, что полученная запись не буква, не слово, а число:
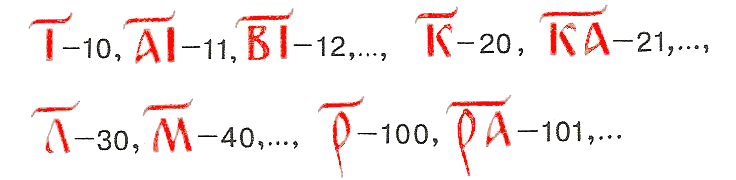 Интересно, что числа от 11 (один-на-десять) до 19 (девять-на-десять) записывали так же, как говорили. То есть "цифру" единиц ставили до "цифры" десятков.
Интересно, что числа от 11 (один-на-десять) до 19 (девять-на-десять) записывали так же, как говорили. То есть "цифру" единиц ставили до "цифры" десятков.
Вывод
В хоже нашего иследования мы узнали, что историю развития натруальных чисел.Выяснили, что раньше записи носили не только счётный характер, но и математический.Так же числа записывали буквами славянского алфавита.
Полезные ресурсы
Математика. 5 класс. Учебник. Мерзляк А.Г., Полонский В.Б., Якир М.С.