Результаты исследования учащихся в проекте Геометрия вокруг нас: различия между версиями
(→Результаты проведённого исследования) |
(→Вывод) |
||
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 72: | Строка 72: | ||
==Вывод== | ==Вывод== | ||
| + | Итак, в ходе нашего исследования, мы узнали много нового. Изучили истоки развития геометрии и познакомились с великими учеными, которые, оказывается, не только изучали геометрию, но и дали толчок развитию других наук. | ||
==Полезные ресурсы== | ==Полезные ресурсы== | ||
| + | |||
| + | *[http://www.apxu.ru/article/geoforma/hi/4_etapa_razvitia_geometrii.htm Этапы развития геометрии]* | ||
| + | |||
| + | *[http://www.mar19654810.narod.ru/p2aa1.html История возникновения геометрии]* | ||
== Другие документы == | == Другие документы == | ||
| − | + | [[Учебный проект Геометрия вокруг нас]] | |
| − | [[ | ||
Текущая версия на 12:54, 23 октября 2013
Содержание
Авторы и участники проекта
- Волкова Мария
- Малышева Анна
- Участники группы: Историки
Тема исследования группы
История геометрии в рамках проекта "Геометрия вокруг нас"
Проблемный вопрос (вопрос для исследования)
С чего начиналась наука геометрия?
Гипотеза исследования
Мы считаем, что геометрия очень увлекательная и своеобразная наука. Одно из её интереснейших сторон - это история её зарождения. Как она зарождалась? Как она процветала? История геометрии помогает нам не только лучше узнать математику, но и углубиться в причины её возникновения и просмотреть исторические моменты развития геометрических знаний у наших предков.
Цели исследования
1.В соответствии с проблемным вопросом изучить истоки возникновения геометрии.
2.Познакомятся с жизнью и деятельностью математиков, внесших вклад в развитие геометрии.
3.Определить временные этапы развития геометрии.
4.Совершить "путешествие" по временным этапам.
Результаты проведённого исследования
Геометрия- наука, изучающая формы, размеры и взаимное расположение геометрических фигур. Она возникла и развивалась в связи с потребностями практической деятельности человека. С древних времён люди сталкивались с необходимостью находить расстояния между предметами, определять размеры участков земли, ориентироваться по расположению звёзд на небе и т. п.
О зарождении геометрии в Древнем Египте около 2000 лет до н. э. древнегреческий историк Геродот писал : " Сезострис, египетский фараон, разделил землю, дав каждому египтянину участок по жребию, и взимал соответствующим образом налог с каждого участка. Случилось,что Нил заливал тот или иной участок, тогда пострадавший обращался к царю,а царь посылал землемеров, чтобы установить,на сколько уменьшился участок, и соответствующим образом уменьшить налог. Так возникла геометрия в Египте, а оттуда перешла в Грецию".
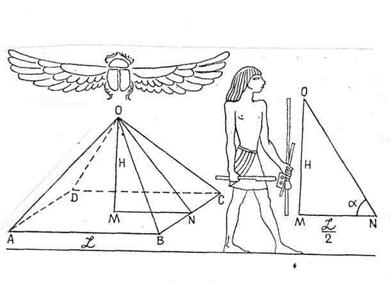
При строительстве даже самых примитивных сооружений необходимо уметь рассчитывать,сколько материала пойдёт на постройку,вычислять расстояния между точками в пространстве и углы между прямыми плоскостями, знать свойства простейших геометрических фигур. Так,египетские пирамиды, сооруженные за 2-3 тысячи лет до н. э., поражают точность своих метрических соотношений, доказывая,что их строители знали многие геометрические положения и расчёты.
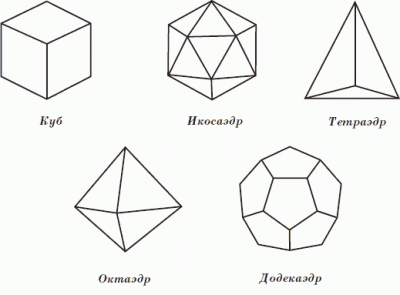
В 5 веке до н. э. центром дальнейшего развития математики становится Южная Италия. Одной из самых известных школ того времени (4-5 вв.до н.э.) являлась пифагорейская, названная так в честь своего основателя- Пифагора. Объясняя устройства мира, пифагорейцы опиралась на математику. Так, выделяя первоосновы бытия, они приписывали их атомам форму правильных многогранников: атомам огня- форму тетраэдра, земли - гексаэдра (куба). воздуха - октаэдра, воды икосаэдра. Всей Вселенной приписывалась форма додекаэдра.
В названиях этих многогранников указывается число граней ( от греческого эдра- "грань"): тетра - "четыри", гекса - "шесть". окта - "восемь", икоса - "двадцать", додека- "двенадцать".
Фалес Милетский . Он мог находить высоту предмета по его тени, пользуясь тем, что треугольник определяется одной стороной и двумя прилежащими к ней углами. Фалес измерил высоту пирамиды, " наблюдая тень пирамиды в тот момент, когда наша тень имеет такую же длину, как и мы сами". Он считал, что отношение высоты вертикально поставленной палки к длине её тени равно отношению высоты пирамиды к длине её тени. Таким образом, Фалесу приписывают теорему о том, что равноугольные треугольники имеют пропорциональные стороны.
Платон не был математиком и не получил никаких результатов в этой науки, но в своих произведениях любил говорить о математике. В частности, в трактате "Тимей" он изложил ученья пифагорейцев о правильных многогранниках, которые благодаря этому впоследствии получили название "платоновых тел".
Евклид жил около 300 года до н. э. К сожалению, о жизни его мало что известно. В одном из своих сочинений математик Папп (3 век до н. э.) изображает его как человека исключительно честного, тихого и скромного, которому были чужды гордость и эгоизм. Насколько серьёзно и строго он относился к изучению математики, можно ссудить по следующий легенде: царь Пталомей спросил у Евклида, нельзя ли найти более короткий и менее утомительный путь к изучению геометрии, чем его "Начала"? Евклид ответил: "В геометрии нет царского пути". Слава Евклиду принесли его "Начала", в котором впервые было представлено стройное аксиоматическое построение геометрии. На протяжение около двух тысячелетий они остаются основой изучения систематического курса геометрии.
В развитии геометрии можно указать четыре основных периода, переходы между которыми обозначали качественное изменение Геометрии.
Первый — период зарождения Геометрии как математической науки — протекал в Древнем Египте, Вавилоне и Греции примерно до 5 в. до н. э. Процесс этот происходил путём накопления новых геометрических знаний, выяснения связей между разными геометрическими фактами, выработки приёмов доказательств и, наконец, формирования понятий о фигуре, о геометрическом предложении и о доказательстве.
Второй - геометрия превратилась в самостоятельную математическую науку: появились систематические её изложения, где её предложения последовательно доказывались. С этого времени начинается второй период развития Геометрии. Здесь Геометрия представлена так, как её в основном понимают и теперь, если ограничиваться элементарной геометрией; это наука о простейших пространственных формах и отношениях, развиваемая в логической последовательности, исходя из явно формулированных основных положений — аксиом и основных пространственных представлений.
Третий - Возрождение наук и искусств в Европе повлекло дальнейший расцвет Геометрии. Принципиально новый шаг был сделан в 1-й половине 17 в. Р. Декартом, который ввёл в Геометрия метод координат. Метод координат позволил связать Геометрия с развивавшейся тогда алгеброй и зарождающимся анализом.
Четвёртый - в развитии Геометрии открывается построением Н. И. Лобачевским в 1826 новой, неевклидовой Геометрии, называемой теперь Лобачевского геометрией.
Вывод
Итак, в ходе нашего исследования, мы узнали много нового. Изучили истоки развития геометрии и познакомились с великими учеными, которые, оказывается, не только изучали геометрию, но и дали толчок развитию других наук.